目标检测非极大值抑制: NMS

2019-09-12

非极大值抑制（Non-Maximum Suppression，NMS），即抑制不是极大值的元素，可以理解为局部最大搜索. 在目标检测中, 无论是 one-stage 或者 two-stage 的算法, 都会得到大量的预测 box, 每个box都会得到一个分数. 但是会存在很多 box 与其他 box 存在包含或者大部分交叉的情况, 即可能同一个目标被多次检测到. 使用 NMS 来去除冗余的预测 box. 如下图: 左图为 nms 之前的box, 右图为 nms 之后的box

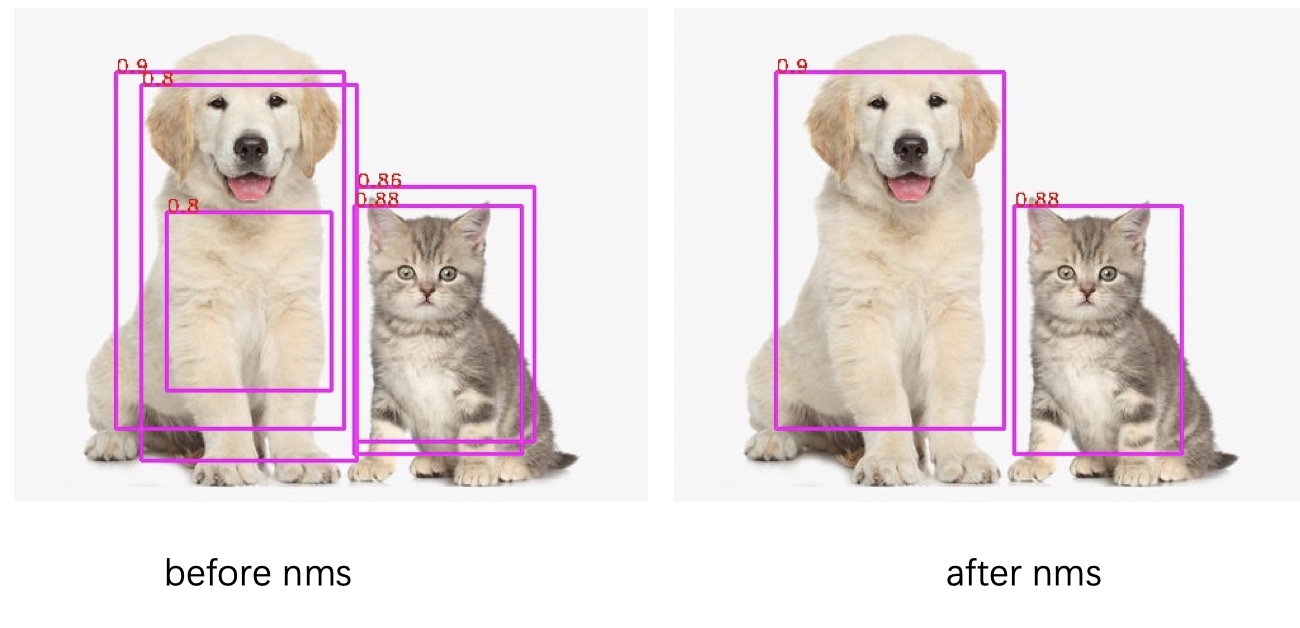
NMS流程

对于得到的 Bounding Box 列 B 及其对应的类别概率 S. 对于每一个类别:

选择具有最大概率的检测框 M, 将其从 box 集合 B 中移除并加入到最终的检测结果 D 中.
计算 B 中每一个剩余框与 M 的IOU, 将 IOU 大于指定阈值的框从 B 中移除. 大于阈值认为是同一目标

重复这个过程,直到 B 为空.

def nms(dests, thresh=0.3, top_k=-1, eps=1e-5):
"""
:param dests: box array  [[x1, y1, x2, y2, score],[x1, y1, x2, y2, score]...]
:param thresh: nms ignore threshold
:param top_k:  keep top_k results. If k <= 0, keep all the results.
:return: picked_box_scores (K, 5): results of NMS.
"""
x1 = dests[:, 0]
y1 = dests[:, 1]
x2 = dests[:, 2]
y2 = dests[:, 3]
scores = dests[:, 4]
areas = (x2 - x1) * (y2 - y1)
order = scores.argsort()[::-1]
keep_box = []

while order.size > 0:
    cur_ind = order[0]
    keep_box.append(dests[cur_ind, :])
    if len(keep_box) == top_k > 0 or dests.shape[0] == 1:
        break

    xlt = np.maximum(x1[cur_ind], x1[order[1:]])
    ylt = np.maximum(y1[cur_ind], y1[order[1:]])
    xrd = np.minimum(x2[cur_ind], x2[order[1:]])
    yrd = np.minimum(y2[cur_ind], y2[order[1:]])

    inter_w = np.maximum(xrd - xlt + 1, 0.0)
    inter_h = np.maximum(yrd - ylt + 1, 0.0)
    inter = inter_h * inter_w
    iou_area = inter / (areas[cur_ind] + areas[order[1:]] - inter + eps)
    # 筛选出 IOU 小于阈值的 box 在 iou_area 中的index, 大于阈值的box作为冗余被去除
    ind = np.where(iou_area <= thresh)[0]
    # 将筛选出的 box 的 index 重新构成 order, iou_area 中 ind 在 order中对应为 ind + 1
    order = order[ind + 1]
return keep_box

IOU 交并比

对于目标检测, IOU 是指两个box 的重叠面积占两个box面积和的比例.

box 的相对位置主要可分为以下四种:

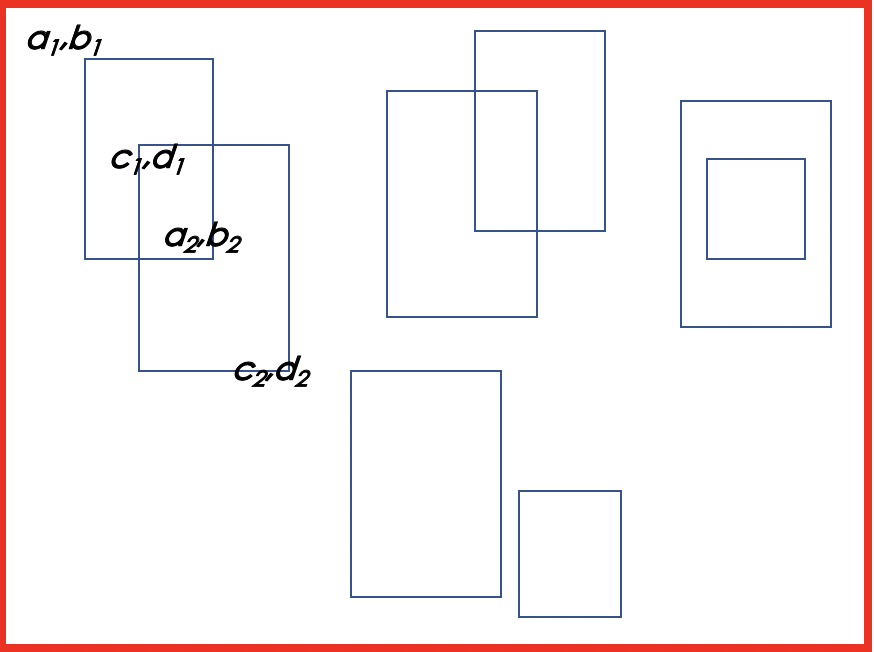
$(a_1, b_1), (a_2, b_2), (c_1, d_1), (c_2, d_2)$ 分别为两个 box 的左上与右下坐标.

重叠区域的左上角$(x _{lt}, y _{lt})$与右下角$(x _{rd}, y _{rd})$坐标可统一为:

$$x _{lt} = max(a_1, c_1)$$ $$y _{lt} = max(b_1, d_1)$$ $$x _{rd} = min(a_2, c_2)$$ $$y _{rd} = min(b_2, d_2)$$ $$w = max(x _{rd} - x _{lt}, 0)$$ $$h = max(y _{rd} - y _{lt}, 0)$$

当两个 box 不相交时, 坐标相减为负值, 置为0.

def iou(box_a, box_b, eps=1e-5):
    """
    :param box_a: [x1, y1, x2, y2]
    :param box_b: [x1, y1, x2, y2]
    :return: iou
    """
    area_boxa = (box_a[2] - box_a[0]) * (box_a[3] - box_a[1])
    area_boxb = (box_b[2] - box_b[0]) * (box_b[3] - box_b[1])

    def intersection(box1, box2):
        x_lt = max(box1[0], box2[0])
        y_lt = max(box1[1], box2[1])
        x_rb = min(box1[2], box2[2])
        y_rb = min(box1[3], box2[3])
        inter_w = max(x_rb - x_lt, 0)
        inter_h = max(y_rb - y_lt, 0)
        return float(inter_w * inter_h)
    area_inter = intersection(box_a, box_b)
    return area_inter / (area_boxa + area_boxb - area_inter + eps)

softnms

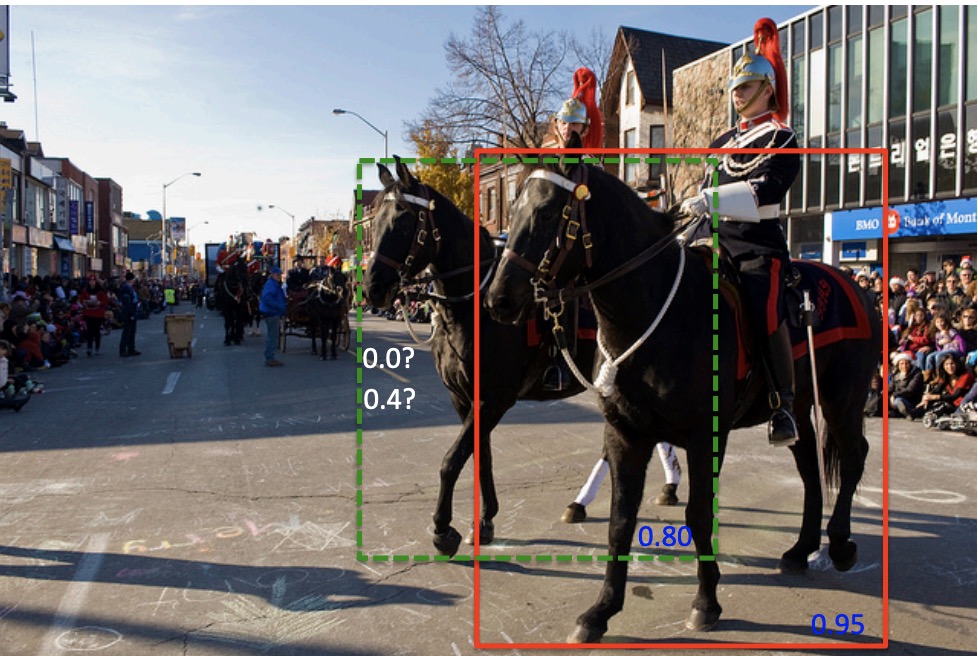
对于上图, 得到两个 box, 目标概率分别为0.9, 0.8。使用 NMS 算法, 设置 0.3 左右的 IOU 会导致绿色框被抑制掉. softnms 则采用降低重叠框的置信度, 重新个重叠框计算目标概率, 最后在根据给定的概率进行过滤.

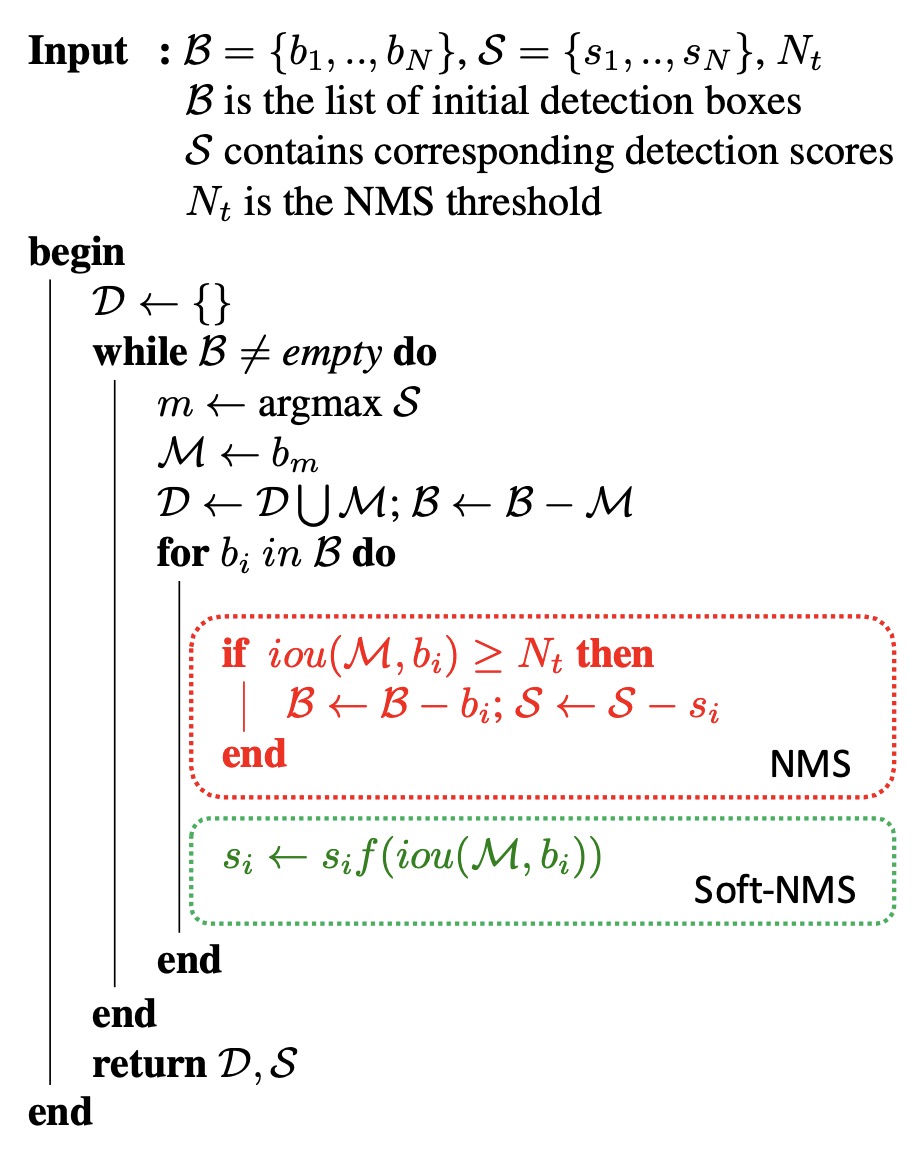
softnms 算法流程如上图, 对于 NMS 是将 IOU 大于给定值得 box 直接丢掉, softnms 则是对 box 进行重新计算 score. 计算完之后, 所有的 box 都在, 然后根据给定的包含目标的概率阈值进行筛选.

算法中计算 $s_i$ 的公式普遍采用以下形式:

$$s_i = s_i e ^{- \frac{iou(M,b_i)^2}{\sigma}}, \forall b_i \not\in D$$

def softnms(dests, obj_thresh, sigma=0.5, top_k=-1, eps=1e-5):
    """
    :param dests: box array  [[x1, y1, x2, y2, score],[x1, y1, x2, y2, score]...]
    :param obj_thresh: object threshold
    :param sigma: the parameter in score re-computation.
                scores[i] = scores[i] * exp(-(iou_i)^2 / simga)
    :param top_k:  keep top_k results. If k <= 0, keep all the results.
    :param eps: a small number to avoid 0 as denominator.
    :return: picked_box_scores (K, 5): results of NMS.
    """
    x1 = dests[:, 0]
    y1 = dests[:, 1]
    x2 = dests[:, 2]
    y2 = dests[:, 3]
    scores = dests[:, 4]
    areas = (x2 - x1) * (y2 - y1)
    order = scores.argsort()[::-1]
    keep_box = []

    while order.size > 0:
        cur_ind = order[0]
        keep_box.append(dests[cur_ind, :])
        if len(keep_box) == top_k > 0 or dests.shape[0] == 1:
            break

        xlt = np.maximum(x1[cur_ind], x1[order[1:]])
        ylt = np.maximum(y1[cur_ind], y1[order[1:]])
        xrd = np.minimum(x2[cur_ind], x2[order[1:]])
        yrd = np.minimum(y2[cur_ind], y2[order[1:]])

        inter_w = np.maximum(xrd - xlt + 1, 0.0)
        inter_h = np.maximum(yrd - ylt + 1, 0.0)
        inter = inter_h * inter_w
        iou_area = inter / (areas[cur_ind] + areas[order[1:]] - inter + eps)
        #   scores[i] = scores[i] * exp(-(iou_i)^2 / simga)
        dests[order[1:], -1] = dests[order[1:], -1] * np.exp(-(iou_area * iou_area) / sigma)
        #   去掉小于 obj_thresh 的 box
        ind = np.where(dests[order[1:], -1] >= obj_thresh)[0]
        order = order[ind + 1]
    return keep_box

目标检测