Reid之路: 度量学习的几种主要loss

度量学习旨在学习两张图片的相似性，那么久需要设计合适的损失函数能让网络提取到更具有判别能力的特征.

contrasitive loss

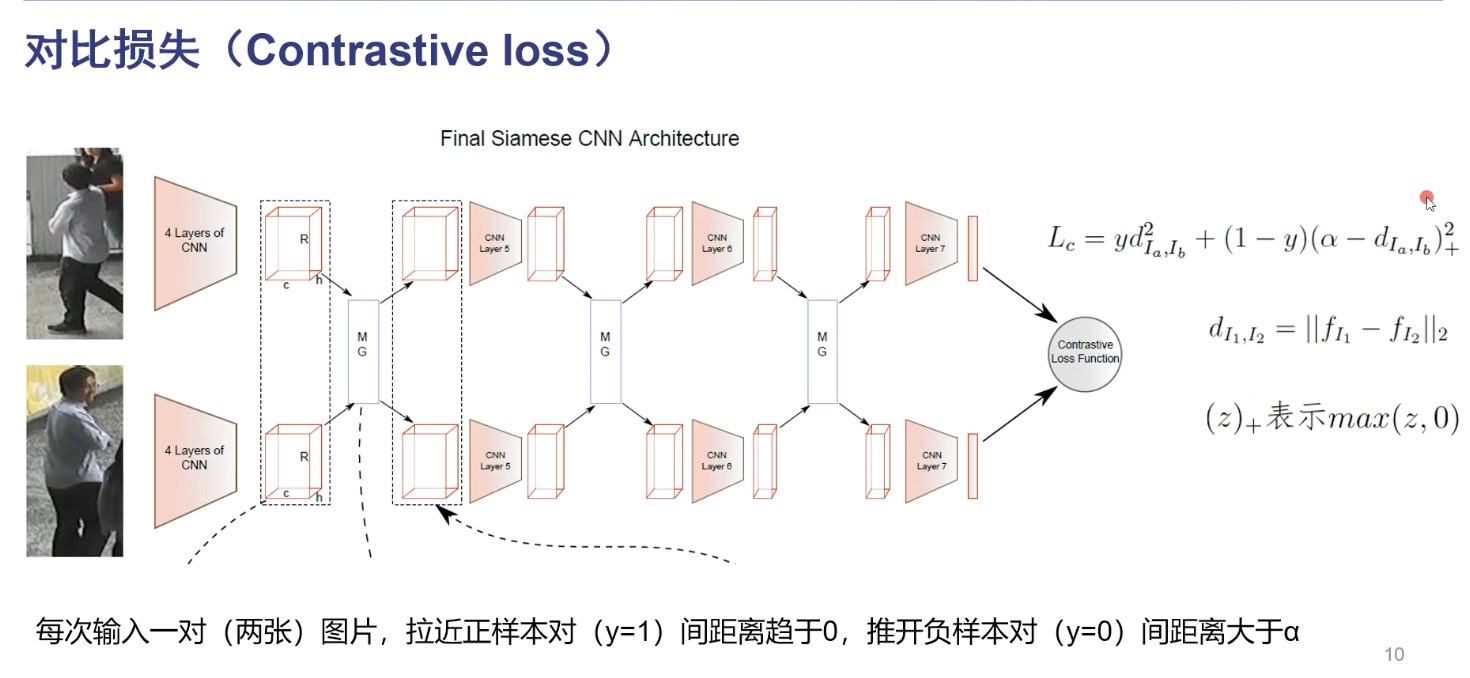
网络优化目标是最小化损失函数 $L _c$, 输入正样本对时， $L _c = yd ^2 _{I _a , I _b}$, 其中 $d$ 为特征向量的 L2 距离. 输入越相似，那么特征理应越相似，L2距离越小. 当输入负样本对时, $y=0$, $$L _c = (\alpha - d ^2 _{I _a , I _b}) ^2 _+$$ $$= max(\alpha - d ^2 _{I _a , I _b}, 0)$$

要最小化损失函数，就要使 $\alpha -d$ 小于0，那么损失即为0, $d ^2 _{I _a , I _b} > \alpha$, 即使负样本对之间的距离要大于 $\alpha$, $\alpha$ 为人工设定的超参, 值设定的越大, 即对判别为负样本对的要求越高. 太大会陷入过拟合. 对比损失拉近正样本对的距离，推开负样本对的距离。

triplet loss

triplet loss 输入三张图片，一张记为 anchor，一张positive(与anchor 同ID)，一张negative(与anchor不同ID), triplet loss 使正样本对的距离小于正样本与负样本对的距离.

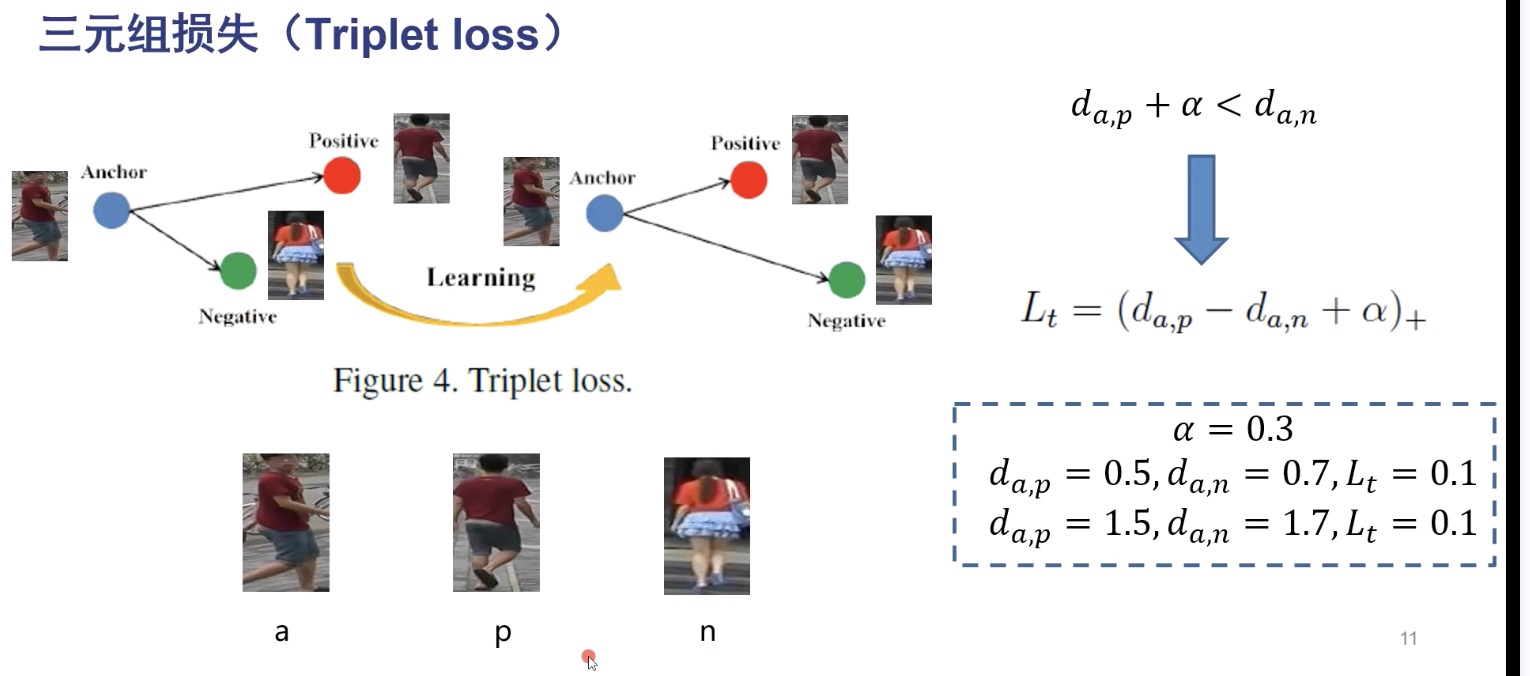
$$L _t = (d _ {a,p} - d _ {a,n} + \alpha) _+$$ $$ = max(d _ {a,p} - d _ {a,n} + \alpha, 0)$$

即使 $d _ {a,p} - d _ {a,n} + \alpha$ 小于0，有 $d _ {a,p} + \alpha < d _ {a,n}$, anchor与positive的距离加上设定的边界值任要小于anchor与negative的距离. $\alpha$ 越大，对正负样本的判别更严苛，太大会过拟合.

传统 triplet loss 只表示了正样本对和正负样本对之间的相对距离，如上图右下角所示，相对距离相同，损失一样. 这样存在弊端：无法卡一个阈值将正负样本明确分开.

改进的triplet loss:

$$L _i t = d _ {a,p} + (d _ {a,p} - d _ {a,n} + \alpha) _+$$

要最小化损失函数，要最小化正样本对之间的距离，还要将正样本对和正负样本的距离拉开.

quadruplet loss

在三元组损失中，只考虑了正样本对、正负样本对的距离，实际上应该使正样本的距离小，正样本对的距离小于正负样本对的距离，还应该拉开负样本的距离.

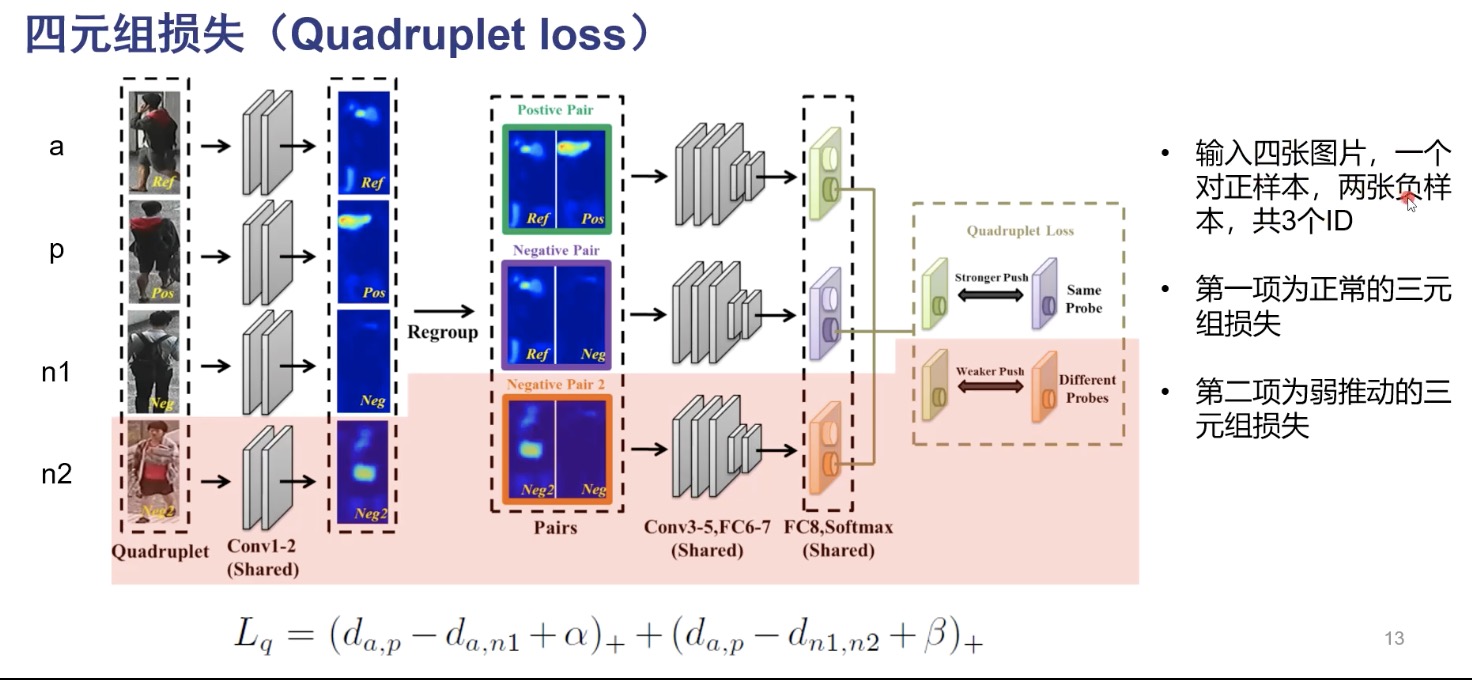
四元组损失输入为四张图片，a、p 来自同一个ID，n1,n2分贝来自不同的ID，使a、p的距离小于a、n1的距离，同时使a、p的距离小于n1、n2的距离，四元组损失第二项包含了绝对距离的.

n-pair loss

对于 triplet loss 参数更新中，只考虑了单个负样本，忽略了其他类的负样本，四元组损失引入了额外的一个负样本与负样本的距离。因而，只能促进query的embedding向量与选中的一个负样本保持较大的距离，但却不能保证与其他未被选择的负样本也保持较大的距离。

常规思路就是每个anchor 同时考虑它与所有负样本的距离，不同于Triplet Loss使用单个的正负样本，N-pair loss损失函数利用了数据之间的结构信息来学习到更有区别性的表示，其在每次参数更新的过程中同时考虑了query样本与其他多个不同类的负样本之间的关系，促使query与其他所有类之间都保持距离，这样能够加快模型的收敛速度。