线性拟合笔记之：Ransac算法

2018-12-19

机器学习

关于Ransac算法

RANSAC为Random Sample Consensus，即随机采样一致性算法，是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据的算法。在计算机视觉中用的比较多，如特征点匹配。本文主要从线性拟合角度分析。

Ransac算法

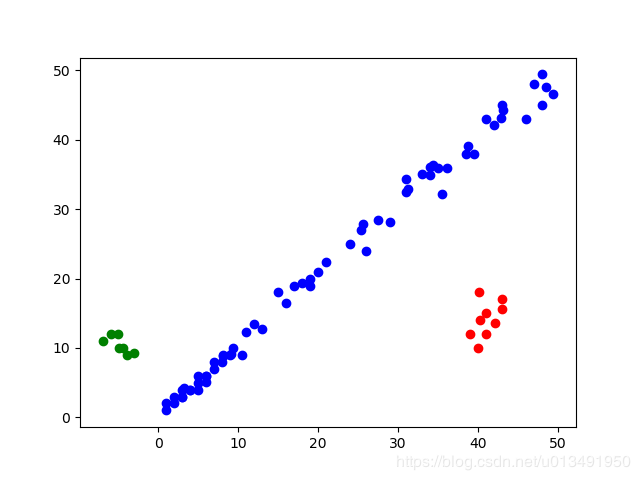
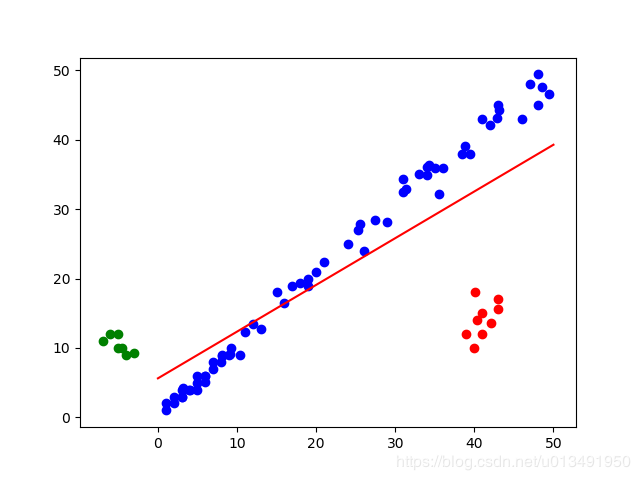
有样本数据集如上图所示，其中蓝色为正确样本，绿色和红色为噪声样本，我们想要拟合一个线性模型，如果使用最小二乘法的话，结果如下图：

对于这个数据样本而言，由于噪声偏离正确数据不是太远且噪声少，拟合结果偏差不是太大。但是当噪声比例或偏离很大时，基于全局的最小二乘法几乎无法得到好的结果。

RANSAC算法的基本假设是样本中包含正确数据(inliers，可以被模型描述的数据)，也包含异常数据(outliers，偏离正常范围很远、无法适应数学模型的数据)，即数据集中含有噪声。主要思想是通过不断的从样本中随机选择一定的样本来拟合模型，然后用未被选中的样本测试模型，根据一定的规则保留最优模型。

算法流程如下

一：随机选择n个样本，作为inliers；二：用inliers拟合一个模型（本文做线性拟合，采用最小二乘），然后用模型测试outliers，如果某个outliers与模型的误差小于给定的阈值，将其加入inliers；三：如果inliers中样本个数大于设定的值，得到认为正确的模型。然后用新的inliers重新估计模型；四：执行以上过程指定的轮数，每次产生的模型要么因为inliers太少而被舍弃，要么比现有的模型更好而被选中。

Ransac线性拟合实验

部分中间迭代结果：

最佳拟合：

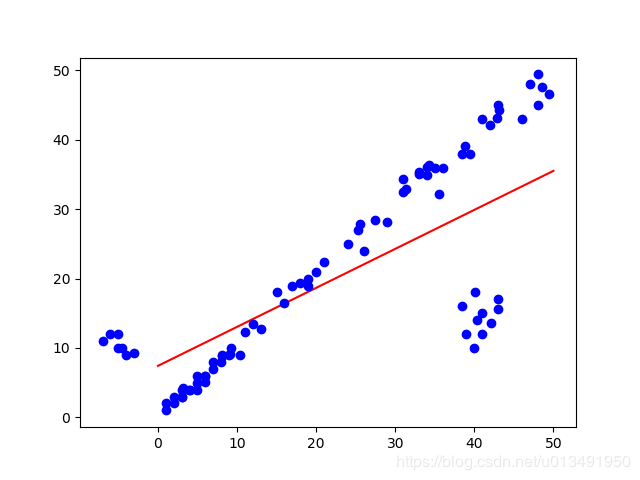
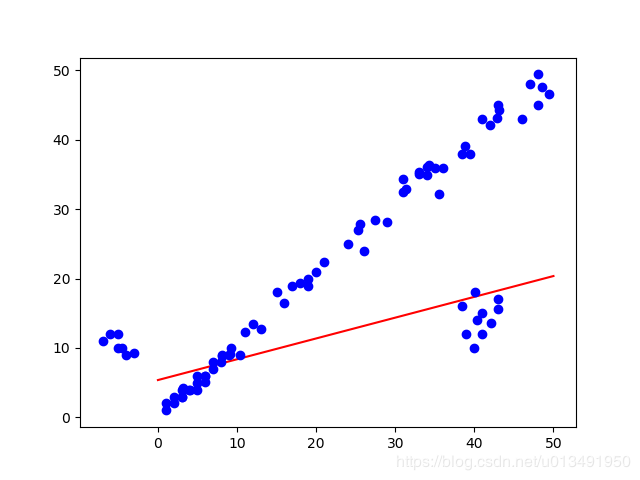
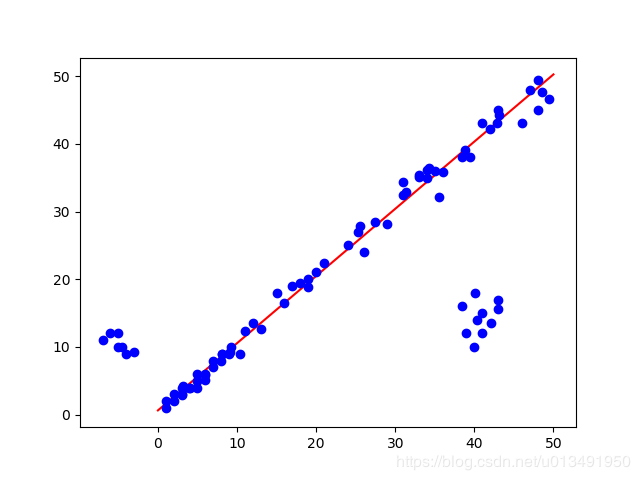
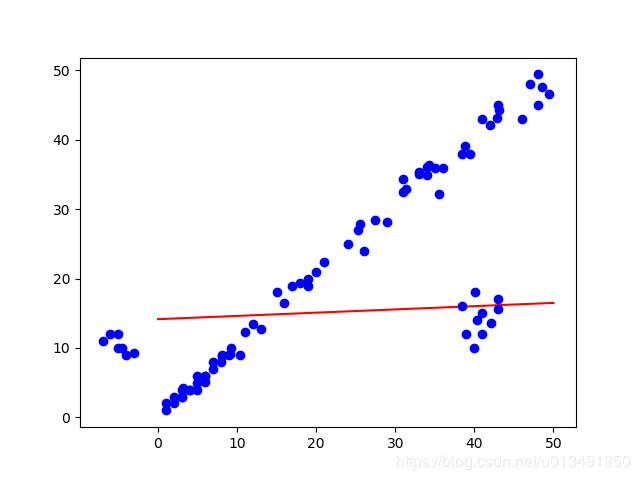
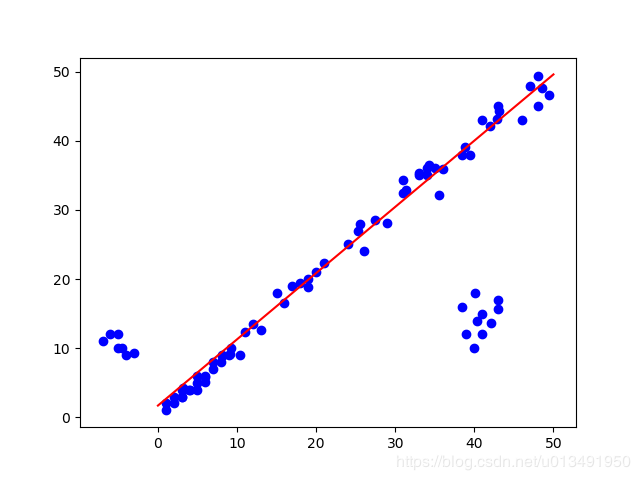
Python代码

import matplotlib.pyplot as plt
from numpy import *
import numpy as np
import operator as op

class Ransac:
    weight = 0.
    bias = 0.

    def least_square(self,samples):
        ##最小二乘法
        x = samples[:,0]
        y = samples[:,1]
        x_ = 0
        y_ = 0
        x_mul_y = 0
        x_2 = 0
        n = len(x)
        for i in range(n):
            x_ = x[i] + x_
            y_ = y[i] + y_
            x_mul_y = x[i] * y[i] + x_mul_y
            x_2 = x[i] * x[i] + x_2
        x_ = x_ / n
        y_ = y_ / n
        weight = (x_mul_y - n * x_ * y_) / (x_2 - n * x_ * x_)
        bias = y_ - weight * x_
        return weight,bias

    def isRepeat(self,sour,tar):
        #判断是否含有重复样本
        for i in range(len(sour)):
            if (op.eq(list(sour[i]), list(tar))):
                    return True
        return False

    def random_samples(self,samples,points_ratio):
        ## 随机采样（无重复样本）
        number = len(samples)
        inliers_num = int(number * points_ratio)
        inliers = []
        outliers = []
        cur_num = 0
        while cur_num != inliers_num:
            seed = np.random.randint(0,number)
            sap_cur = samples[seed]
            if not self.isRepeat(inliers,sap_cur):
                cur_num = cur_num +1
                inliers.append(list(sap_cur))
        for i in range(number):
            if not self.isRepeat(inliers,samples[i]):
                outliers.append(list(samples[i]))
        return np.array(inliers),np.array(outliers)

    def fun_plot(self,sample,w,b):
        data_x = np.linspace(0, 50, 50)
        data_y = [w * x + b for x in data_x]
        plt.ion()
        plt.plot(data_x,data_y,'r')
        plt.plot(sample[:,0],sample[:,1],'bo')
        plt.show()
        plt.pause(0.05)
        plt.clf()

    def ransac(self,samples, points_ratio = 0.05, epoch = 50, reject_dis = 5 ,inliers_ratio = 0.4):
        # samples 输入样本，形如 [[x1 ,yi],[x2, y2]]
        # point_ratio  随机选择样本点的比例
        # epoch    迭代轮数
        # reject_dis  小于此阈值将outliers加入inliers
        # inliers_ratio  有效inliers最低比例

        inliers_num_cur = 0
        for i in range(epoch):
            inliers,outliers = self.random_samples(samples,points_ratio)
            weight_cur,bias_cur = self.least_square(inliers)
            # self.fun_plot(samples,weight_cur,bias_cur)
            for j in range(len(outliers)):
                distance = np.abs((weight_cur* outliers[j,0]+ bias_cur) - outliers[j,1]) / np.sqrt(np.power(weight_cur,2)+1)
                if distance <=  reject_dis:
                    inliers = np.vstack((inliers,outliers[j]))
            weight_cur,bias_cur = self.least_square(inliers)
            self.fun_plot(samples,weight_cur,bias_cur)
            if len(inliers) >= len(samples)* inliers_ratio:
               if len(inliers) > inliers_num_cur:
                    self.weight = weight_cur
                    self.bias = bias_cur
                    inliers_num_cur = len(inliers)


test = Ransac()
sample = np.loadtxt('sample.txt')
test.ransac(sample)
data_x = np.linspace(0,50,50)
data_y = [test.weight * x +test.bias for x in data_x]
plt.plot(sample[:, 0], sample[:, 1], 'bo')
plt.plot(data_x,data_y,'r')
plt.show()
plt.pause(3)

参考：百度百科

ransac