线性拟合笔记之:最小二乘法
关于最小二乘法
以下是百度百科的解释:最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。 对于线性拟合,给定的具有线性关系的观测样本,可以通过最小二乘法求解得到线性模型。
一元线性回归模型求解
给定的观测数据 :(x1,y1),(x2,y1),(x3,y3)……(xn,yn),假设其存在着线性关系,线性模型为:$$ \bar{y} = wx +b $$
优化目标函数为:
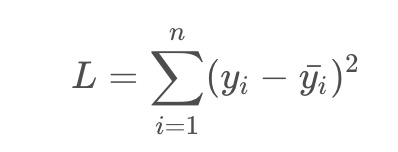
即标签值和预测值之间的均方误差,所选择的回归模型应该使所有观察值的残差平方和达到最小,
也就是 Least square。
将目标函数展开:
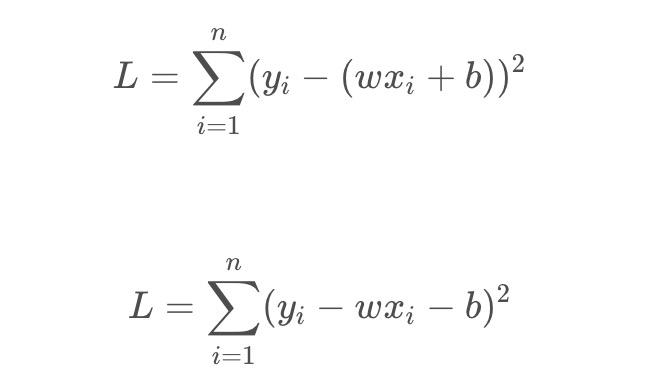
此时,L是关于w 和 b 的函数,要使 L的值最小,由数学知识可知,可以通过求偏导令为0可解得,即:
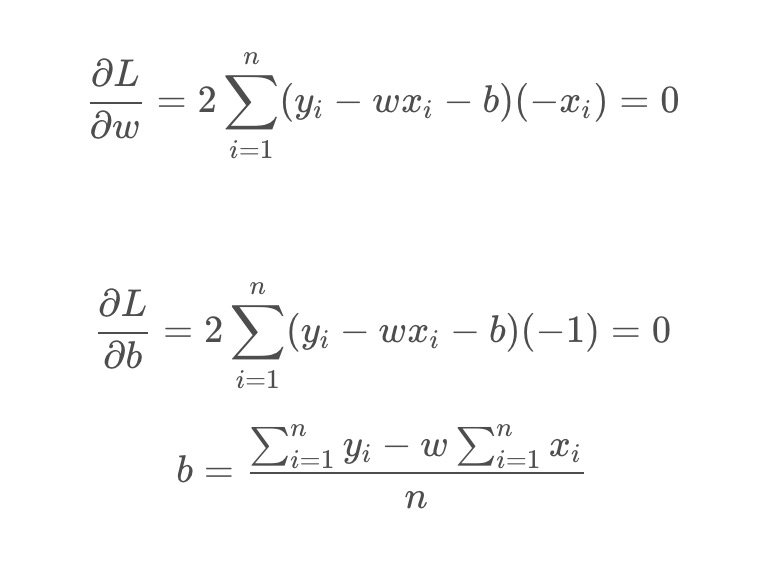
记:
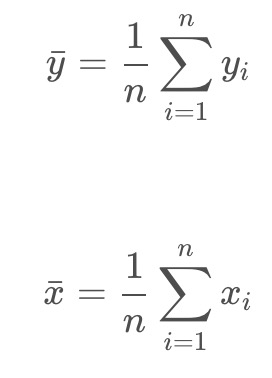
则 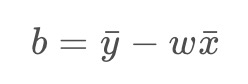
同理可得:
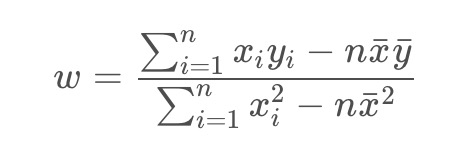
即可求得w,b。
最小二乘实现
一元最小二乘法
由上面的 w 可以看出,整个计算结果依赖于$\bar{x}$,$\bar{y}$,$x{i}y{i}$,$x_{i}^{2}$
python测试代码如下:
import matplotlib.pyplot as plt
import numpy as np
class Least_square:
weight = 0
bias = 0
def get_weight(self):
return self.weight
def get_bias(self):
return self.bias
def least_square(self,x,y):
if len(x)!= len(y):
print('data error')
return
x_ = 0
y_ = 0
x_mul_y = 0
x_2 = 0
n = len(x)
for i in range(n):
x_ = x[i] + x_
y_ = y[i] + y_
x_mul_y = x[i]*y[i] + x_mul_y
x_2 = x[i]*x[i] + x_2
x_ = x_ / n
y_ = y_ / n
self.weight = (x_mul_y - n*x_*y_)/(x_2 - n*x_*x_)
self.bias = y_ - self.weight*x_
def fun_plot(self):
data_x = np.linspace(0,10,20)
data_y = [self.weight * x +self.bias for x in data_x]
print('y='+str(self.weight)+'x+'+str(self.bias))
plt.plot(data_x,data_y)
plt.show()
test = Least_square()
x = np.array([1,2,3,6,1.5,4,7,4.3,9.2])
y = np.array([2,1.5,4,7,1.8,5.3,8.6,5.6,11])
plt.plot(x,y,'ro')
test.least_square(x,y)
test.fun_plot()
运行结果示例:
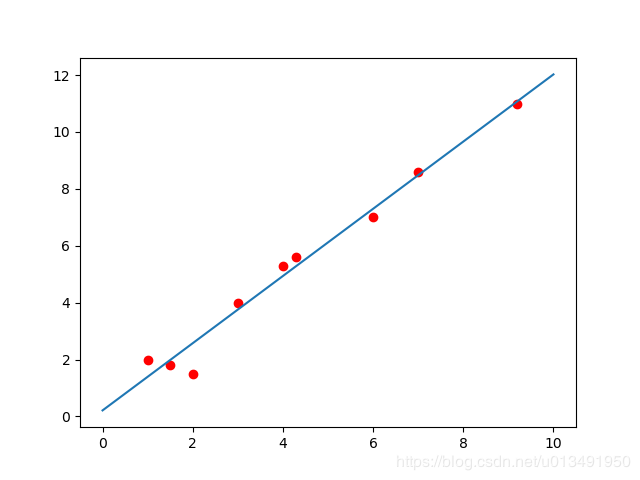 因为最小二乘法是对所有数据进行拟合,寻找到所有点的误差最小的直线,当数据不存在大的异常点时,效果应该是很好的。
如下图,当增加一个明显的异常点(蓝色点)时,拟合的直线会靠向异常点
因为最小二乘法是对所有数据进行拟合,寻找到所有点的误差最小的直线,当数据不存在大的异常点时,效果应该是很好的。
如下图,当增加一个明显的异常点(蓝色点)时,拟合的直线会靠向异常点
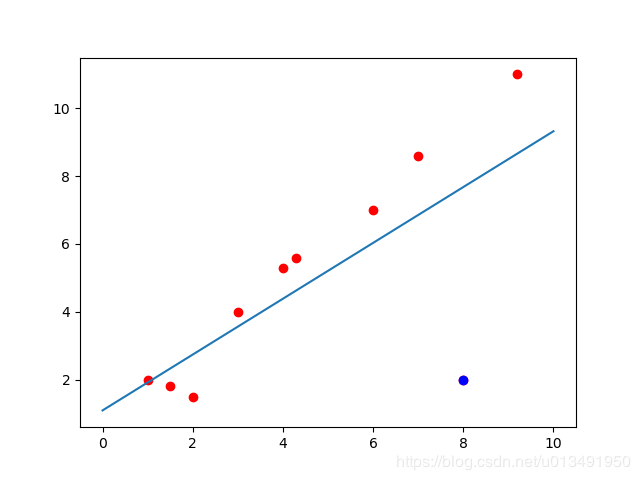
多元线性回归模型
百度百科:在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
记多元线性回归模型为:
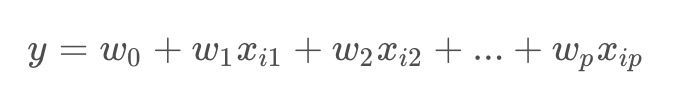
已有的观测数据:(x1,y1),(x2,y1),(x3,y3)……(xn,yn)
最小化残差平方和函数:
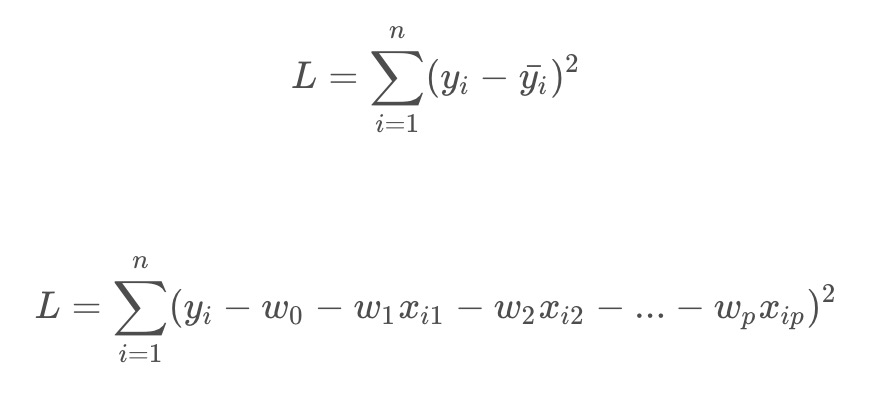
求偏导:
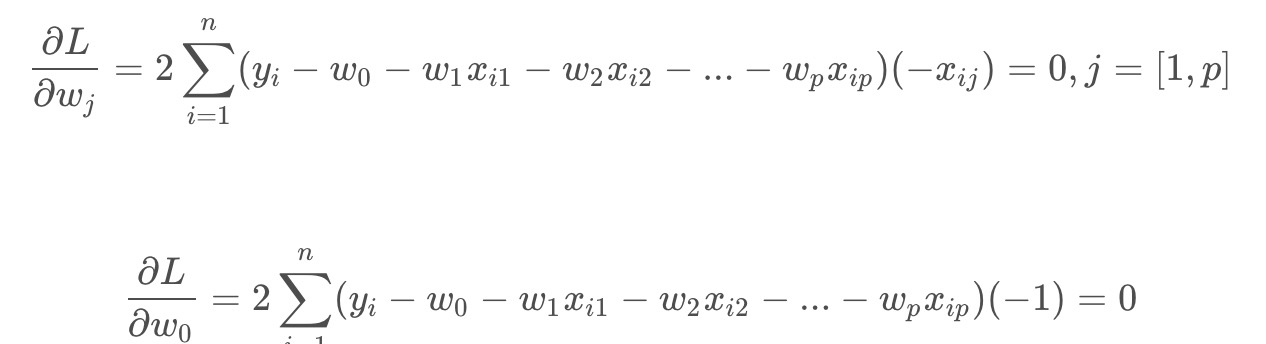
然后写成:
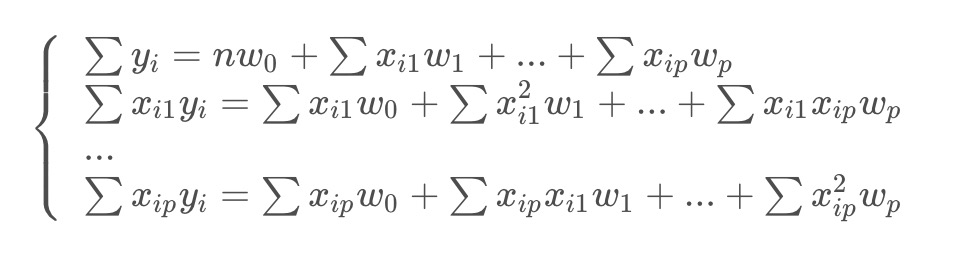
矩阵形式:
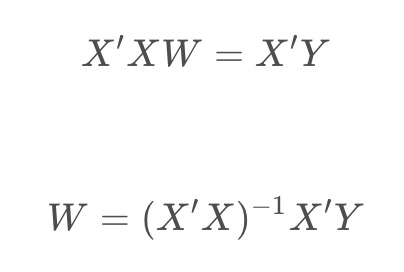
这是一个通用的形式,管它几元都行。写成这样的形式,用numpy的mat计算就更方便了,代码就更简单了(前段时间的网易笔试题就让编多元最小二乘,哎,自己推半天,还错了,哈哈),数学真的太重要了!!!
(从CSDN迁移过来的,公式不对,懒得打。。。)
参考:1.百度百科

