识别损失函数汇总
在之前的文章中记录了部分用于重识别的损失,主要是基于欧式距离的损失,本文接着对人脸识别使用的损失进一步做个小结.
首先,针对于识别任务,不论是什么损失,主要可以从以下几个方面出发考虑:
- 深度学习的特征需要具有discriminative(判别性)和泛化能力,以便在没有标签预测的情况下识别新的未见类别,如一个人脸即便没有训练过也能判断类别。判别性同时表征了紧凑的类内差异和可分离的类间差异。
- 判别性特征可以通过最近邻(NN)或k近邻(k-NN)算法进行良好分类,其不一定取决于标签预测。
- 原始的softmax损失仅鼓励特征的可分离性,所得到的特征对于人脸识别不是足够有效的。
center losspaper
中心损失:在训练时为每个类别记录类别中心,训练时最小化每个样本与该类别中心的距离,缩小类内距离。
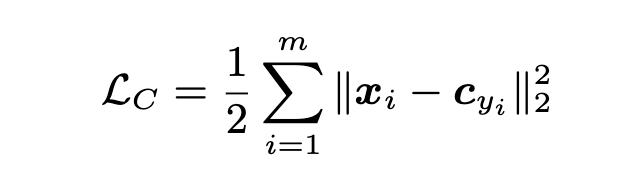
center loss 公式如上,x 是网络输出的feature,C 是某个类别的中心,即最小化该类别和类别中心的距离。
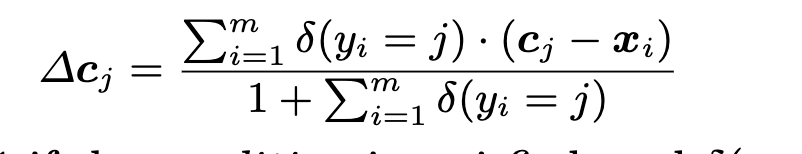
类别中心的更新公式,同时类别中心一般随机初始化,训练过程中根据每个batch的输出feature进行更新,有点像BN那种统计全局信息的味道.
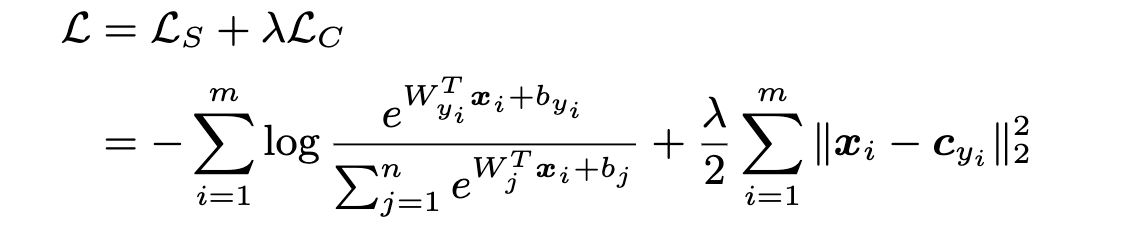
将 softmax loss 与center loss 作为联合监督损失.
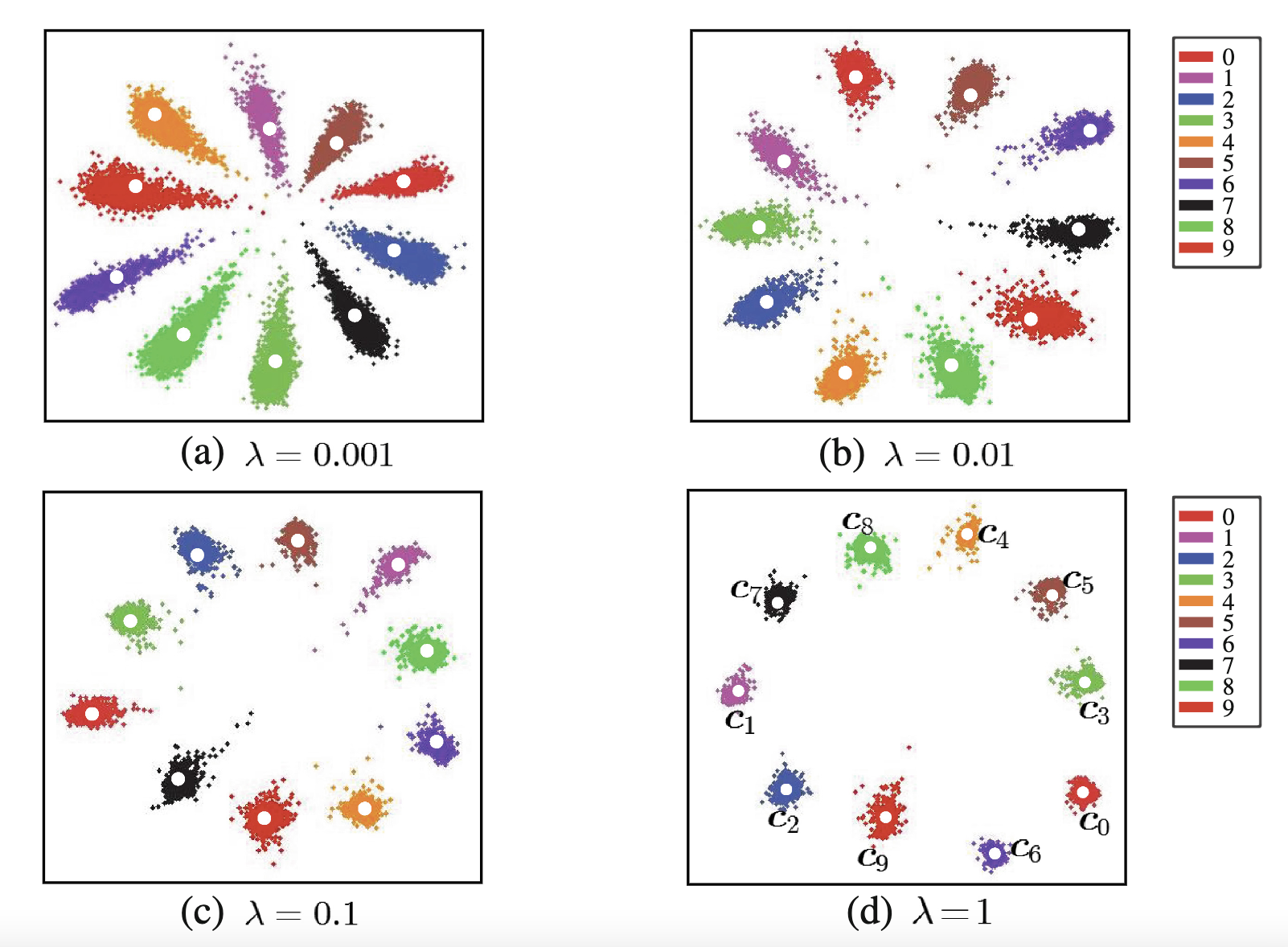
不同的中心损失系数下的学到的特征分布示意图, center loss比重越大,类内越聚合,判别能力越大
基于 softmax 的改进
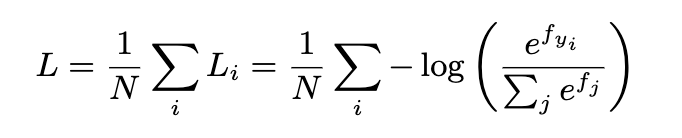
softmax 损失形式如上图,softmax可以使类间分开,但是不能有效的使类内特征内聚,而基于softmax的改进损失函数,主要从两个方面:
- 增加类间间隔
- 类内内聚
公式中的 $f_{yi}$ 可以写层向量形式,即
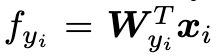
其中 W 为全连接层权重,由于 f 是 W 和 X 的内积,因此可以写成:
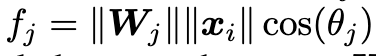
转化到角度空间,对于一个二分类问题,要是输入 X 分为第一类,那么有
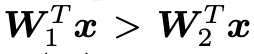
等价于
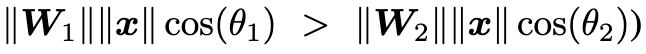
L-Softmax loss paper
由上诉 softmax 公式可知,分类的概率依赖于向量的模和夹角,L-softmax 通过增加一个正整数变量m,从而产生一个决策余量,能够更加严格地约束上述不等式
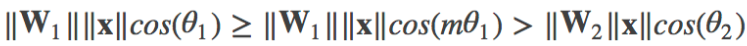
由于 cos(x) 在 0-π 之间单调减,m值越大(θ1会更加小)使得模型可以学到类间距离更大的,类内距离更小的特征,同时学习的难度也越大
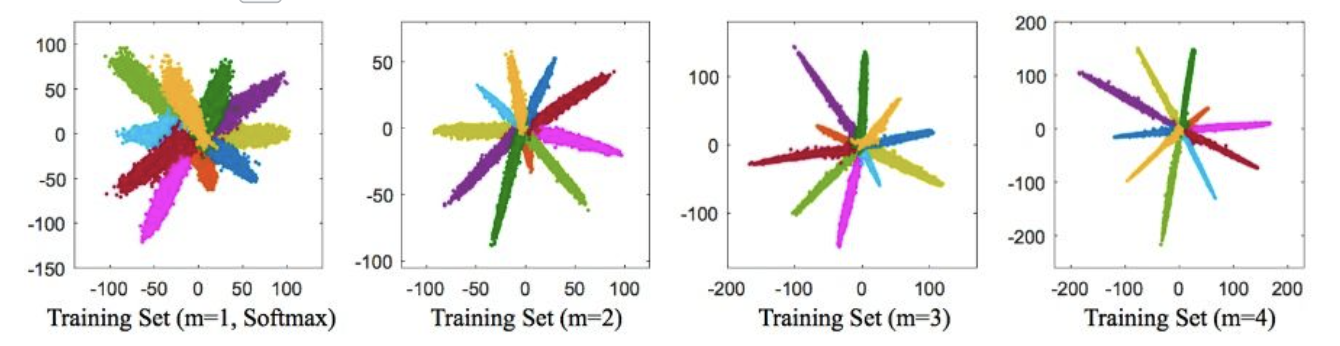
A-softmax paper
A-Softmax(Angular Softmax loss):在L-Softmax loss的基础上做权重归一化和偏置项归零(||W_i||=1,b_i=0),使得预测仅取决于W和x之间的角度
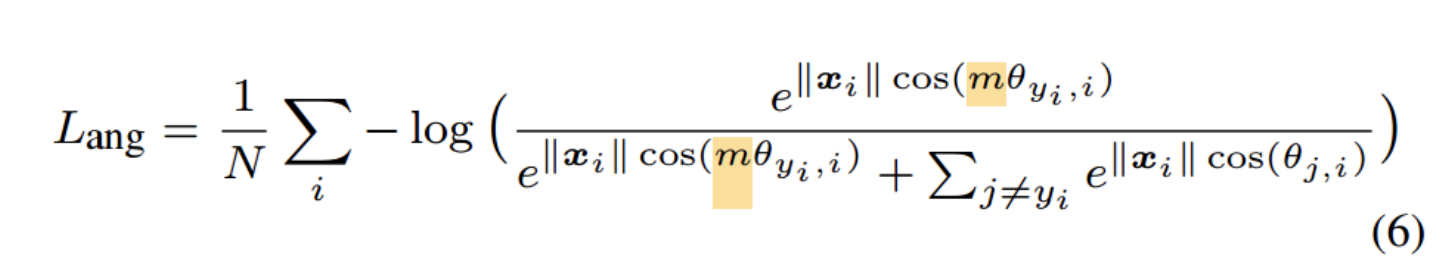
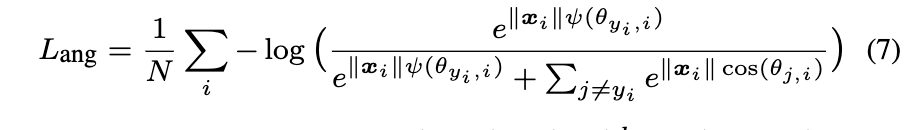
CosFace paper
CosFace Loss也称Large Margin Cosine Loss (LMCL)(也是AMSoftmax):additive cosine margin,让cos(θ)加上m,m是cosine margin
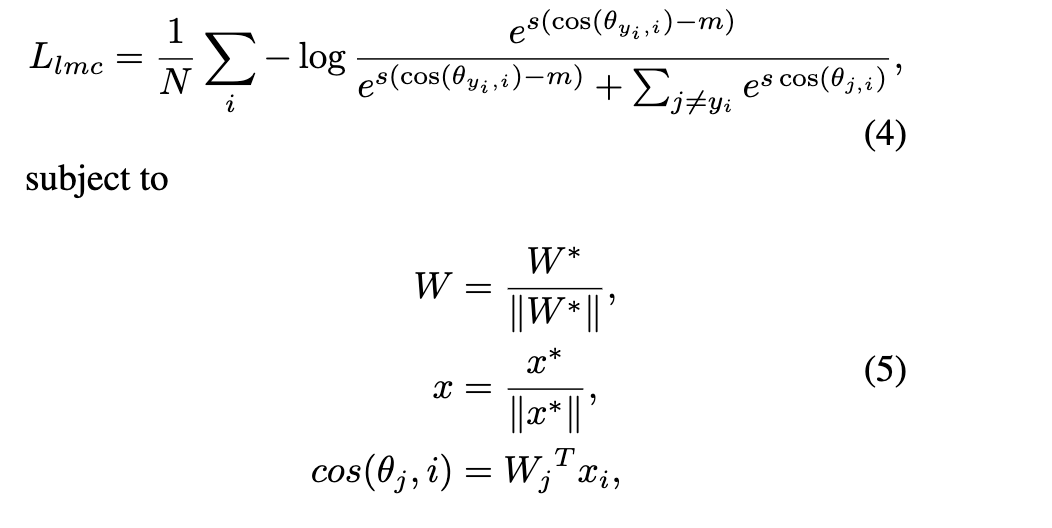
决策边界变为:
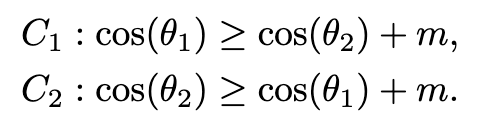
ArcFace paper
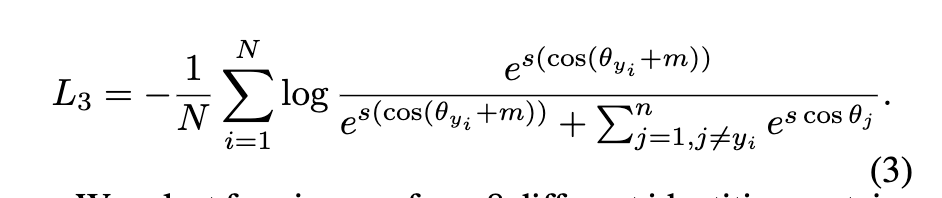
- ArcFace loss:Additive Angular Margin Loss(加性角度间隔损失函数),在xi和Wji之间的θ上加上角度间隔m(注意是加在了角θ上),以加法的方式惩罚深度特征与其相应权重之间的角度,从而同时增强了类内紧度和类间差异。角度间隔比余弦间隔在对角度的影响更加直接。几何上有恒定的线性角度margin。
- ArcFace中是直接在角度空间θ中最大化分类界限,而CosFace是在余弦空间cos(θ)中最大化分类界限。
- 特征向量和权重归一化:L2归一化来修正单个权重||W_j||=1,还通过L2归一化来固定嵌入特征||x_i|,并将其重新缩放成s。特征和权重的归一化步骤使预测仅取决于特征和权重之间的角度。

