深度学习归一化: BN,LN,IN,GN

深度学习中的常见归一化方法主要有: batch Normalization, layer Normalization, instance Normalization, group Normalization.

神经网络学习过程的本质就是为了学习数据分布, 如果没有做归一化处理, 那么每一批次训练数据的分布不一样, 网络需要在这多个分布中找到平衡点, 对于每层每层网络而言, 同样当输入数据分布在不断变化, 这也会导致每层网络在找平衡点, 因此神经网络就很难收敛了.

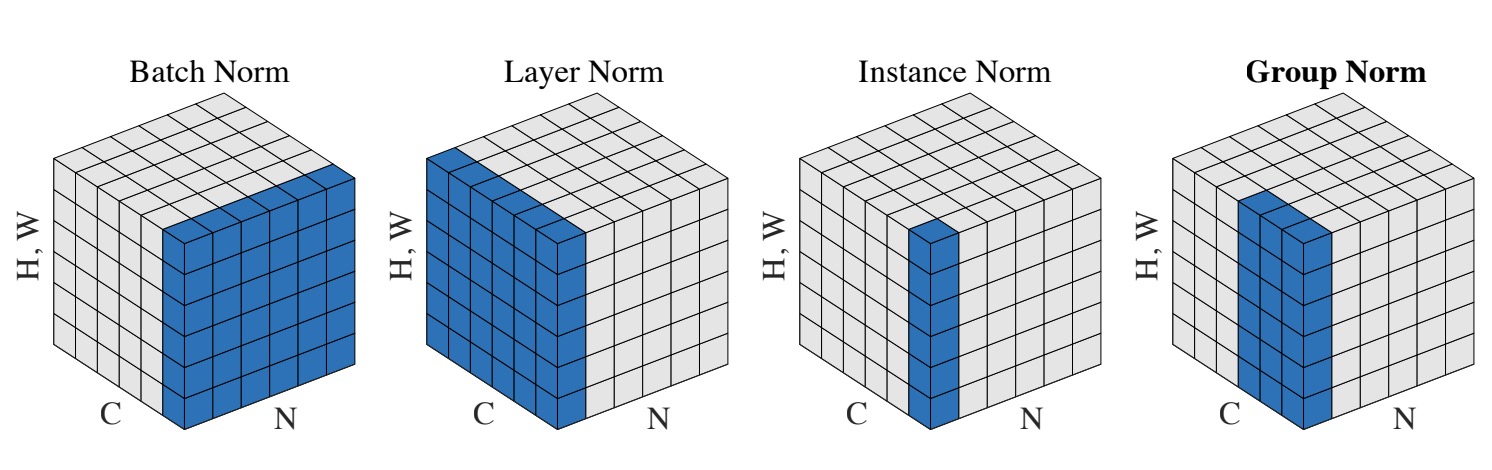
四者的对比如下图来自论文GN, 假设输入数据为[N,C,H,W], 为了便于图示, 将HW放在一起, 对图像而言相当于将二维图片拉成一行:

batch Normalization

即批量归一化, 如上图所示, 在 batch 方向进行归一化, 对输入的batchsize的训练样本, 沿batch方向对所有样本的各个通道分别归一化. 从而保证数据分布的一致性, 而对于基于CNN的判别判别模型的结果正是取决于数据整体分布, BN对batchsize的大小比较敏感, 由于每次计算均值和方差是在一个batch上, 所以如果batchsize太小, 则计算的均值、方差不足以代表整个数据分布.

# 模拟BN
def bn(x):
    b, c, h, w = x.shape
    gamma = torch.rand((c,))
    beta = torch.rand((c,))
    for i in range(c):
        # 逐通道归一化
        mean = x[:, i, :, :].mean()
        std = x[:, i, :, :].std()
        x[:, i, :, :] = (x[:, i, :, :] - mean) / (std + 1e-5)
        x[:, i, :, :] = x[:, i, :, :] * gamma[i] + beta[i]
    return x

$\gamma$ 与 $\beta$ 作为可学习参数重构输入. pytorch 中训练时以动量的方式更新均值和方差, 测试时直接使用. $\hat X _{new} =(1- m) * \hat X + m * X _t$, m 为设置的动量参数, $X _t$ 为当前batchsize的均值, $\hat X$ 为估计的统计值, $\hat X _{new}$ 为新的估计均值, 方差情况类似.

layer Normalization

对输入每一层的每一个样本进行归一化

def ln(x):
    b, c, h, w = x.shape
    gamma = torch.rand((b,))
    beta = torch.rand((b,))
    for i in range(b):
        mean = x[i, :, :, :].mean()
        std = x[i, :, :, :].std()
        x[i, :, :, :] = (x[i, :, :, :] - mean) / (std + 1e-5)
        x[i, :, :, :] = x[i, :, :, :] * gamma[i] + beta[i]
    return x

instance Normalization

IN 主要用于GAN网络中, 比如画风迁移、图像生成等, 图片生成的结果主要依赖于某个图像实例自己, 使各个实例保持独立.

def In(x):
    b, c, h, w = x.shape
    gamma = torch.rand((b, c))
    beta = torch.rand((b, c))
    for i in range(b):
        for j in range(c):
            mean = x[i, j, :, :].mean()
            std = x[i, j, :, :].std()
            x[i, j, :, :] = (x[i, j, :, :] - mean) / (std + 1e-5)
            x[i, j, :, :] = x[i, j, :, :] * gamma[i, j] + beta[i, j]
    return x

group Normalization

GN 先将 channel 分组, 然后类似于IN对各个组的数据进行归一化, 相当于与引入了通道间的依赖.