图像去雾: Single Image Haze Removal Using Dark Channel Prior

2020-04-03

图像增强

此论文是何凯明博士在2009CVPR上的发表的论文, 在图像增强领域可谓无人不知. 论文的方法主要基于对无雾室外图像的统计. 本文主要对原文以及参考Github 上的代码进行理解

论文思想

在计算机视觉中, 带雾图像被建模为:

$$I(x) = J(x)t(x) + A(1-t(x)), (1)$$

其中, I(x) 为观测到的强度即待去雾图像, J(x）为要恢复的无雾图像, A(x) 是全球大气光成分. t(x) 为透射率. 图像去雾的目标则是从中恢复出 J, A, t.

暗通道先验基于以下对室外无雾图像的观测: 在大多数非天空局部区域中, 有一些像素至少在一个颜色通道有非常低的强度. 换言之，这些区域的最小强度是很低的值. 形式化如下:

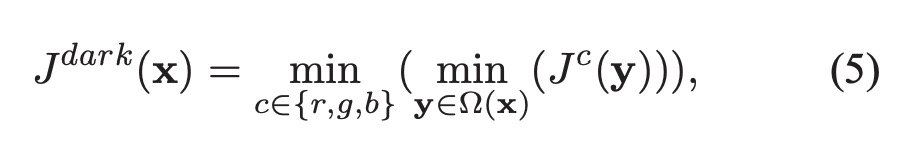
Ω(x) 表示以 x 为中心的区域. 区域大小可指定, 求此区域的暗通道相当于在整个RGB通道对该区域进行最小值滤波. 作者通多大量观测得到结论: 如果J 是室外无雾图像, 除开天空区域 $J ^{dark}$ 应该是很小的值，趋近于0.

暗通道中的低强度主要归因于三个因素：a）阴影. 例如，城市景观图像中的汽车，建筑物和窗户内部的阴影，或景观图像中的叶子，树木和岩石的阴影； b）彩色物体或表面。例如，任何颜色通道中缺少颜色的任何对象（例如，绿草/树木/植物，红色或黄色的花/叶和蓝色的水面）都会导致暗通道中的值降低； c）深色物体或表面。例如深色的树干和石头。由于自然的室外图像通常充满阴影和色彩，因此这些图像的暗通道真的很暗！

代码来源

无雾图片暗通道如下图所示:

带雾图片暗通道如下:

透射率估计

先假设全球大气光成分A已知。同时假定以x 为中心的局部区域 Ω(x) 透射率是常量. 由公式1 对局部区域进行进行最小操作, 最小操作独立的在三个通道进行.

等价于

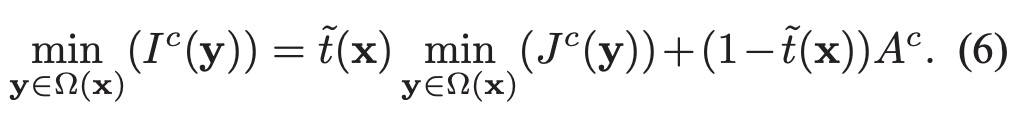
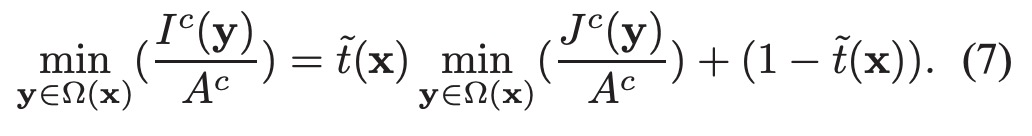
在三个通道上取最小值可得:

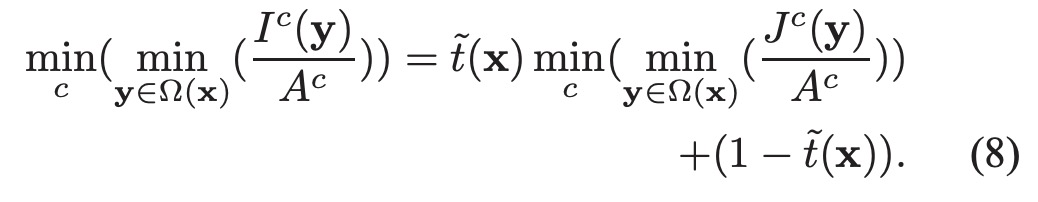
根据暗通道先验理论, 无雾图像的暗通道幅度趋于0:

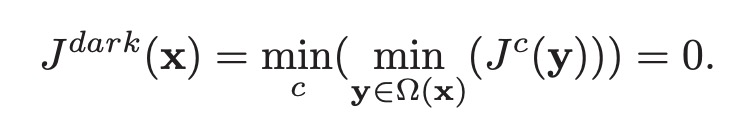
$A ^c$ 恒为正数, 因此:

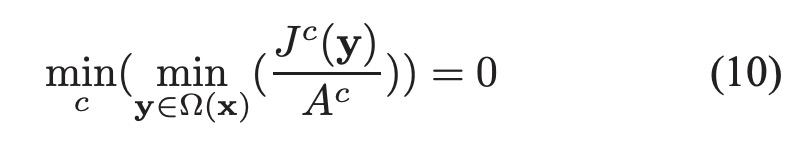
将（10）代入（8）可得透射率的预估值:

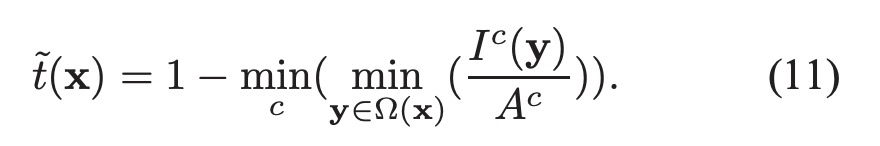
考虑到在现实生活中，即使是晴天白云，空气中也存在着一些颗粒，因此，看远处的物体还是能感觉到雾的影响，另外，雾的存在让人类感到景深的存在，因此，有必要在去雾的时候保留一定程度的雾, 上式修正为, ω 设为0.95:

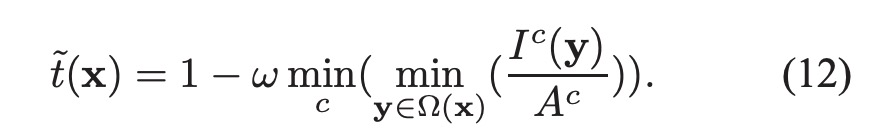
估计全球大气光

文中表明带雾图像的暗通道很好地近似了雾密度, 借助于暗通道图来从有雾图像中估计全球大气光:

从暗通道图中按照亮度的大小取前0.1%的像素。
在这些位置中，在原始有雾图像I中寻找对应的具有最高亮度的点的值，作为A值。

恢复图像

在已经有了I，A，t 的情况下，便可以求得J。

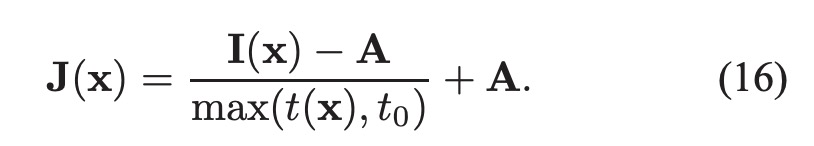
其中, $t _0$ 用来防止 $t(x)$ 过小而导致的 J 过亮.

示例

code

import cv2
import math
import numpy as np


def dark_channel(im, sz):
    # 暗通道计算
    b, g, r = cv2.split(im)
    # 取每个像素位置RGB三通道中的最小值
    dc = cv2.min(cv2.min(r, g), b)
    kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (sz, sz))
    # 进行最小值滤波
    dark = cv2.erode(dc, kernel)
    return dark


def atm_light(im, dark):
    # 计算全球大气光的值
    [h, w] = im.shape[:2]
    imsz = h * w
    numpx = int(max(math.floor(imsz / 1000), 1))
    darkvec = dark.reshape(imsz, 1)
    imvec = im.reshape(imsz, 3)

    indices = darkvec.argsort()
    indices = indices[imsz - numpx::]

    atmsum = np.zeros([1, 3])
    # 使用前0.1%的均值, 而不是最大值
    for ind in range(1, numpx):
        atmsum = atmsum + imvec[indices[ind]]

    A = atmsum / numpx
    return A


def transmission_estimate(im, A, sz):
    # 按照公式（12）计算
    omega = 0.95
    im3 = np.empty(im.shape, im.dtype)
    for ind in range(0, 3):
        im3[:, :, ind] = im[:, :, ind] / A[0, ind]

    transmission = 1 - omega * dark_channel(im3, sz)
    return transmission


def guided_filter(im, p, r, eps):
    # http://kaiminghe.com/eccv10/index.html
    mean_I = cv2.boxFilter(im, cv2.CV_64F, (r, r))
    mean_p = cv2.boxFilter(p, cv2.CV_64F, (r, r))
    mean_Ip = cv2.boxFilter(im * p, cv2.CV_64F, (r, r))
    cov_Ip = mean_Ip - mean_I * mean_p

    mean_II = cv2.boxFilter(im * im, cv2.CV_64F, (r, r))
    var_I = mean_II - mean_I * mean_I

    a = cov_Ip / (var_I + eps)
    b = mean_p - a * mean_I

    mean_a = cv2.boxFilter(a, cv2.CV_64F, (r, r))
    mean_b = cv2.boxFilter(b, cv2.CV_64F, (r, r))

    q = mean_a * im + mean_b
    return q


def transmission_refine(im, et):
    gray = cv2.cvtColor(im, cv2.COLOR_BGR2GRAY)
    gray = np.float64(gray) / 255
    r = 60
    eps = 0.0001
    t = guided_filter(gray, et, r, eps)
    return t


def recover(im, t, A, tx=0.1):
    # 公式(16)
    res = np.empty(im.shape, im.dtype)
    t = cv2.max(t, tx)
    for ind in range(0, 3):
        res[:, :, ind] = (im[:, :, ind] - A[0, ind]) / t + A[0, ind]
    return res


if __name__ == '__main__':

    src = cv2.imread("1.png")
    I = src.astype('float64') / 255
    dark = dark_channel(I, 15)
    A = atm_light(I, dark)
    te = transmission_estimate(I, A, 15)
    t = transmission_refine(src, te)
    J = recover(I, t, A, 0.1)

    cv2.imshow("dark", dark)
    cv2.imshow("t", t)
    cv2.imshow('I', src)
    cv2.imshow('J', J)
    cv2.imwrite("J.png", J * 255)
    cv2.waitKey()

ref

paper

cnblogs图像去雾算法的原理、实现、效果

图像去雾