剑指offer7:重构二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路: 对于二叉树,其前序遍历为(根左右),中序为(左根右). 依次取前序序列的节点为当前根节点,可以将中序遍历结果划分为左子树,根节点,右子树.
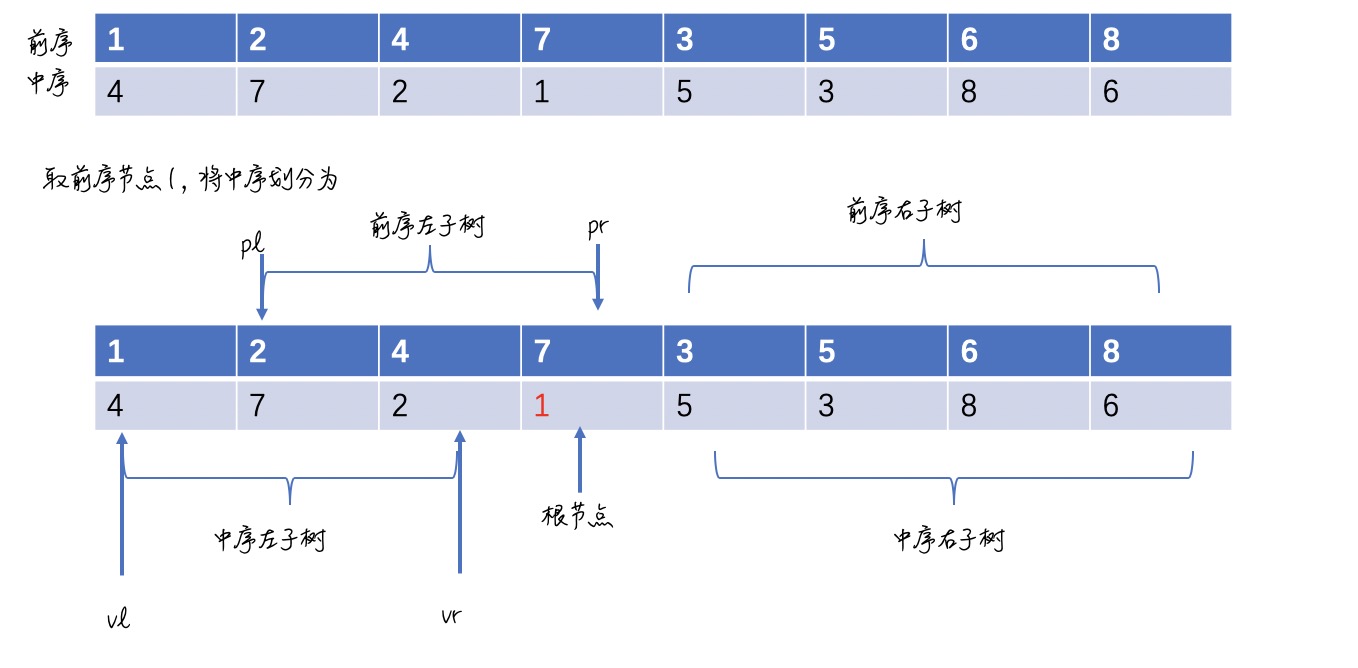
如图所示,每次取前序遍历的第一个节点,可得到此节点的左右子树,对其左右子树,其构造过程和其相同,因此,可通过递归,每次取前序第一个节点将其划分为构造左右子树,当其为叶子节点时停止递归. 题目主要难点在左右子树的起始和终止节点的设置.
#include <vector>
using namespace std;
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
TreeNode* build_tree_node(vector<int> pre, vector<int> vin, int pl, int pr, int vl, int vr){
TreeNode* node = new TreeNode(pre[pl]);
//当前序左边界和前序右边界均指向此节点时,为叶子节点
if(pl == pr){
return node;
}
int index = 0;
//记录当前根节点在中序中的位置
while(vin[index]!=pre[pl]) index++;
int k = index -vl;
//k为左子树的长度
if(k > 0){
node->left = build_tree_node(pre, vin, pl + 1, pl + k, vl, vl +k -1);
}
// 根节点index不等于中序右边界,即为存在右子树
if(index < vr){
node->right = build_tree_node(pre, vin, pl + k +1, pr, index+1, vr);
}
return node;
}
TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
if(pre.size()==0 || pre.size()!=vin.size()){
return nullptr;
}
return build_tree_node(pre, vin, 0, pre.size()-1,0, vin.size()-1);
}
int main(){
vector<int> pre = {1,2,4,7,3,5,6,8};
vector<int> vin={4,7,2,1,5,3,8,6};
TreeNode* root = reConstructBinaryTree(pre, vin);
return 1;
}

