从RNN到LSTM小记
记录自己对LSTM结构的理解,以及结合keras在实现LSTM模型时数据的输入数据等的处理。
1.SimpleRNN
对于多层感知机网络而言,是假设每个输入数据具有独立性。如训练图像分类网络时,每次根据输入图片计算误差更新网络权重,当前输入图像不会对后续输入产生影响。但是对于时序数据而言,如翻译、天气预测、股票预测等,此时输入数据之间具有相关性。因此我门希望网络能够记住当前数据的关键信息,并用之于后续数据,以此循环。
RNN用隐藏状态或记忆引入后序数据对前面数据的依赖,以保存当前关键信息。
理论结合实际最好理解,因此下文都基于:给出前7天的天气数据,希望预测出接下来一天的温度.
则RNN结构图如下:
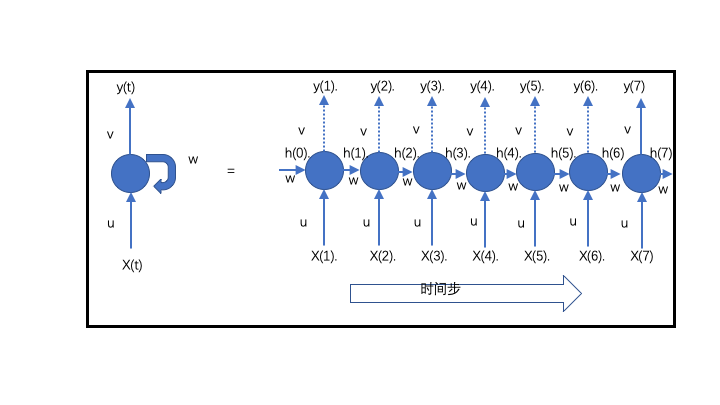
RNN可图形化为左图的结构,其中
- X(t)为时间步t的输入数据,即每一天的天气数据特征(特征具体是什么暂时不考虑)
- y(t)为对应时间步的输出。同时,输出的一部分(隐藏状态h(t))反馈给神经单元,以在接下来的时间步t+1使用。即隐藏状态使序列信息得到保留以作用于下一个输入。
- u,v,w为权重矩阵。
可记为:
$$h(t) = tanh(W*h(t-1) + U*x(t))$$
$$y(t) = relu(V*h(t))$$
为了便于更加形象的理解,都倾向于将RNN按时间步展开(因为我们要使用7天的数据预测一天的温度,故时间步为7,因此展开为7个。同时只需要一个输出,因此将前6个的输出都标记为为虚线,即在7个时间步数据上进行处理后只有最后一步会得到一个输出)。在7个时间步上,u、v、w均是”共享”的(但这么说不太准,后面细说),而信息由隐藏态h(t)进行在时间步上传递。
由于展开更加形象,往往会导致误解一个RNN模块由多个左图构成(😄我以前就犯了这种错).谨记:展开只是为了便于理解,实际上不管时间步有多少,一个RNN模块只有左边一个结构,所以上面说的共享不太确切(本身就是它自己). 具体来说就是,输入了7天的天气数据给RNN,RNN首先处理x(1)的数据得到h(1),然后又处理x(2)的数据…,RNN模块都是同一个。为什么强调这个问题呢,因为在写代码定义RNN的时候,如keras指定units,并不是指定有多少个RNN模块,而是一个RNN模块它的神经元个数。
2.LSTM
长短期记忆(Long short-term memory, LSTM)是RNN的变体之一,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。
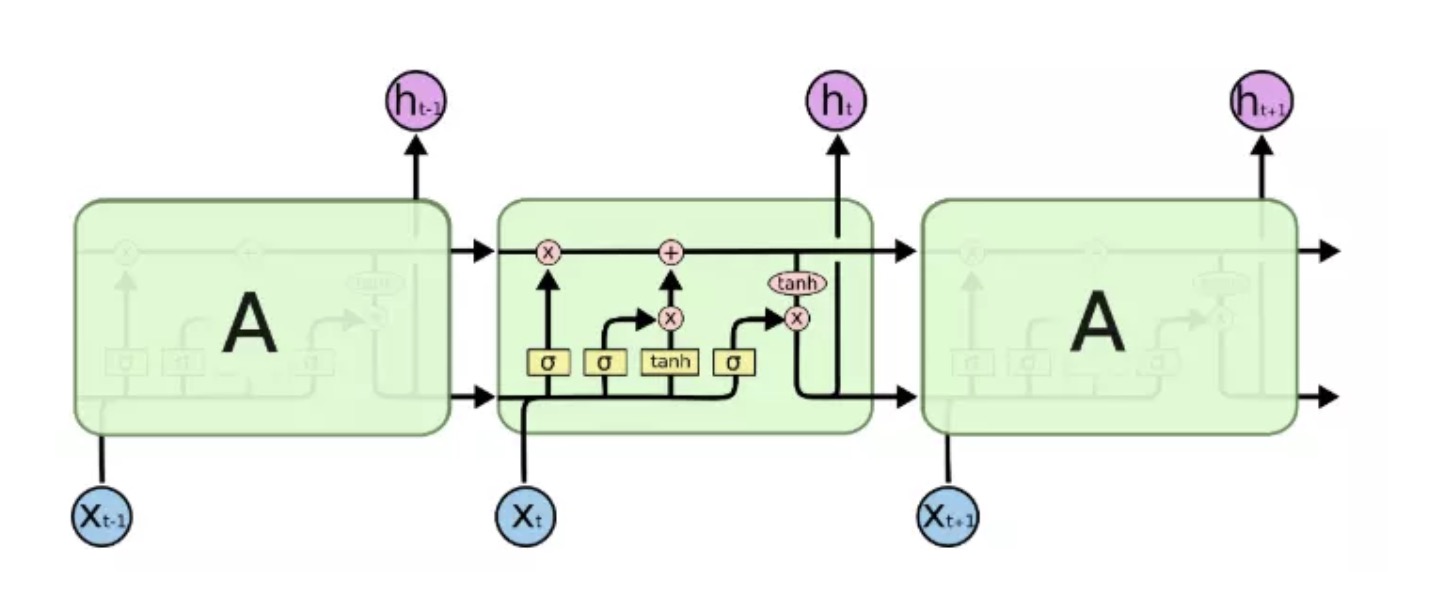
LSTM 按3个时间步展开如上图所示. LSTM单元内部结构比RNN更加复杂。LSTM单元内部结构如下图:
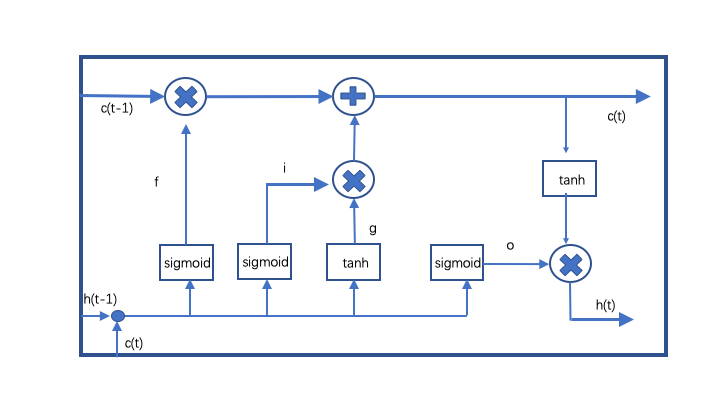
其中:
- i–输入门: $$i = sigmoid(Wi*[h(t-1),x(t)] + bi)$$
- f–遗忘门: $$f = sigmoid(Wf*[h(t-1, x(t)] + bf)$$
- o–输出门: $$o = sigmoid(Wo*[h(t-1, x(t)] + bo)$$
- $$g = tanh(Wg*[h(t-1),x(t)] + bg)$$
- $$c(t) = c(t-1).* f + g.* i$$
- $$h(t) = tanh(c(t)) .* o$$
i,f,o三者通过sigmoid激活函数转换成0到1之间的数值,来作为一种门控状态.sigmoid函数调节这些门使其输出0和1之间的值,将产生的输出向量与另一个向量进行元素乘,以决定第二个向量有多少部分可以通过. g则是将结果通过tanh激活函数将转换成-1到1之间的值,g输入数据,而不是门控信号。 LSTM中具有两个状态,c(t)为长期记忆单元:变化慢,由c(t-1)加上一些数值,h(t)为短期记忆单元:不同节点下往往会有很大的区别。
1.忘记阶段: 遗忘门定义了h(t-1)传进来的输入有多少可以通过。简单来说就是会 “忘记不重要的,记住重要的”。遗忘门设为0时表示忽略所有就记忆。
2.选择记忆阶段: 输入门定义为当前输入x(t)新计算出来的状态有多少可以通过。
3.输出阶段:这个阶段输出门将决定哪些将会被当成当前状态的输出。
对比于RNN,LSTM通过门控状态来控制传输状态,记住需要长时间记忆的,忘记不重要的信息;而不像普通的RNN那样只能够简单的记忆叠加。对很多需要“长期记忆”的任务来说,尤其好用。
3.LSTM参数计算
当我们在代码中定义了一个LSTM层时,只包含一个LSTM模块。实例如下:假设每天的天气数据只包含温度,即根据前7天的温度预测接下来一天的温度(😁当然实际这么做没意义),即一个时间步只有一个特征。
在keras中LSTM的输入数据格式为(samples, timesteps,features),samples相当于CNN中batch_size,本文中timesteps为7,features为每个时间步的特征纬度,此处为1.
由第二部分LSTM的计算公式可以知道,参数来自于i、f、o、g,假设设置LSTM units为128,此时的128指的是i、f、o、g各具有128个神经元。同时,LSTM是全连接,所以必须知道features的纬度(在CRNN中就有)。
因此,参数计算公式为:(units * (units + features) + units) * 4.
第一units代表每个部分具有的神经元个数,第二个units代表的隐层h的输出纬度(由o的公式可知,与神经元个数相同),features是特征纬度,第三个units是bias(多少个神经元,多少个bias). 因为是全连接,因此units * (units + features).
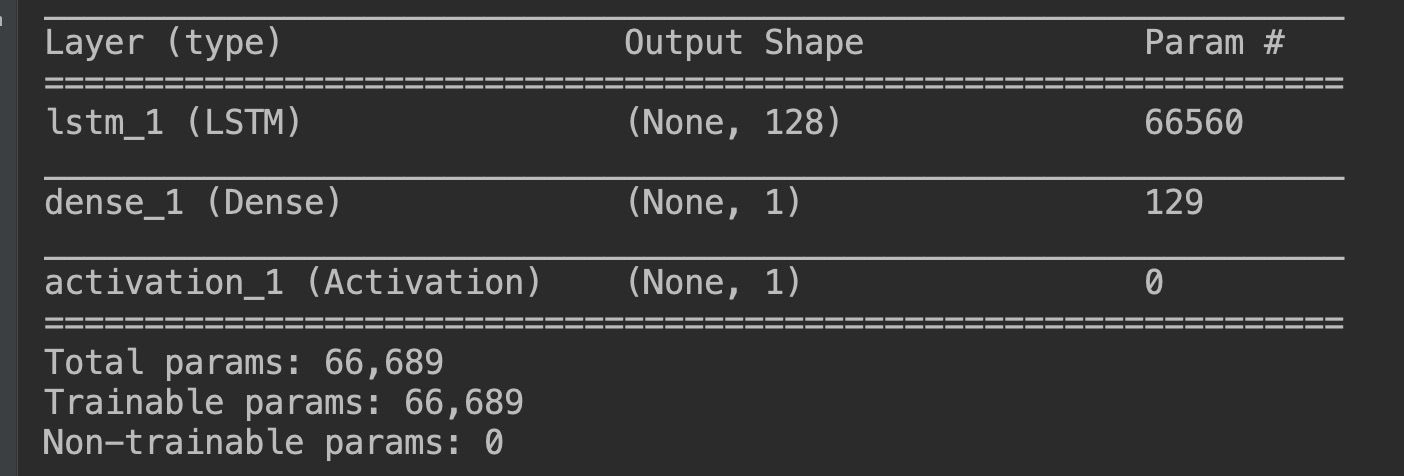
# 本例中,假设units 128, features 1, 公式可得一层LSTM参数为 66560
n_timesteps = 7
n_features = 1
model = Sequential()
model.add(LSTM(128, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(Dense(1))
model.add(Activation("relu"))
model.summary()
运行结果(多试了几个,没毛病😄):
4.keras LSTM 输入
第一次使用LSTM的时候,关于输入数据的格式纠结了很久,主要是自己的观念没有从图像转过来,理解之后和CNN其实一个道理。
在keras中,LSTM输入数据是3D的–(samples, timesteps, features).
- samples为样本个数,即为Batch_size
- timesteps为时间步数,即控制一个LSTM单元在一个样本上会执行多少次。对于序列数据而言,即依赖于前多少个数据。比如我们用7天预测之后一天,时间步即为7.用5天即为5.
- features为每一个时间步的特征的纬度,此处的纬度为一维向量(所以在将LSTM和CNN结合时都需要将CNN输出flatten). 本例中假如只根据前7天的温度来预测之后一天的温度.那么每一天的特征只有温度,则features为1. 引入更多特征,features即为特征向量的长度。
因此,当features为1时,每个样本的数据格式为(7,1)数组即可.若每次输出一个样本,使用numpy.reshape,将输入reshape为(1, 7, 1)即可.
# 假如每个时间步,特征纬度为1,一个样本数据如下
data = np.array([1, 2, 3, 4, 5, 6, 7])
data = np.reshape(data, (1, 7, 1))
# 特征纬度为3,一个样本的数据格式如:
# shape(7, 3)
data = [[1, 2, 3],
[2, 4, 6],
[4, 3, 5],
[7, 5, 9],
[1, 2, 3],
[6, 3, 9],
[3, 5, 7]]
# 若一次要训练多个样本,如samples=4,则读取的data shape为(28,3)
data = np.array(...)
data = np.reshape(data, (4, 7, 3))

