Focal loss
intro
主流的目标检测网络主要包含两种架构,一种是先进行region proposal再分别对得到的region 进行分类与边框回归的 two-stage 网络, RCNN 及其衍生. 另一种是以YOLO, SSD 为代表的one-stage 网络. 对于 two-stage 网络而言, 其送往检测器的 proposal 数量已经在几百到1k的数据级, 且这些 proposal 偏向于对应真实的物体, 非背景. 但是对于one-stage 的目标检测器而言, 他们往往会预测很多的 box, 但是大多数box对应的都是背景, 正真的物体只是少数. 如 yolo-v3 检测 10647 个box, ssd300 检测 7308 个box. 对这些box进行分类, 网络偏向于预测成背景类
focal loss
focal loss 被设计来解决 one-stage 目标检测场景下困难样本检测难的问题,同时也对解决前景背景分类样本不平衡的有所帮助.
记二值交叉熵函数:
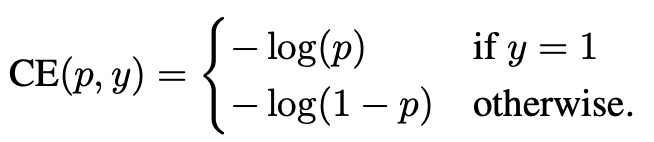
$y \in { 1, -1 }$ 指定GT类别, $p \in [0, 1]$ 为 $y=1$ 时模型的预测概率. 定义 $p_t$:
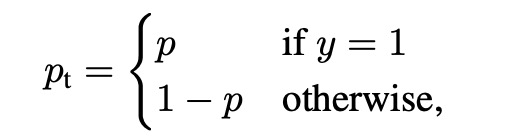
重写交叉熵函数为 $CE(p,y)=CE(p_t)=-log(p_t)$.
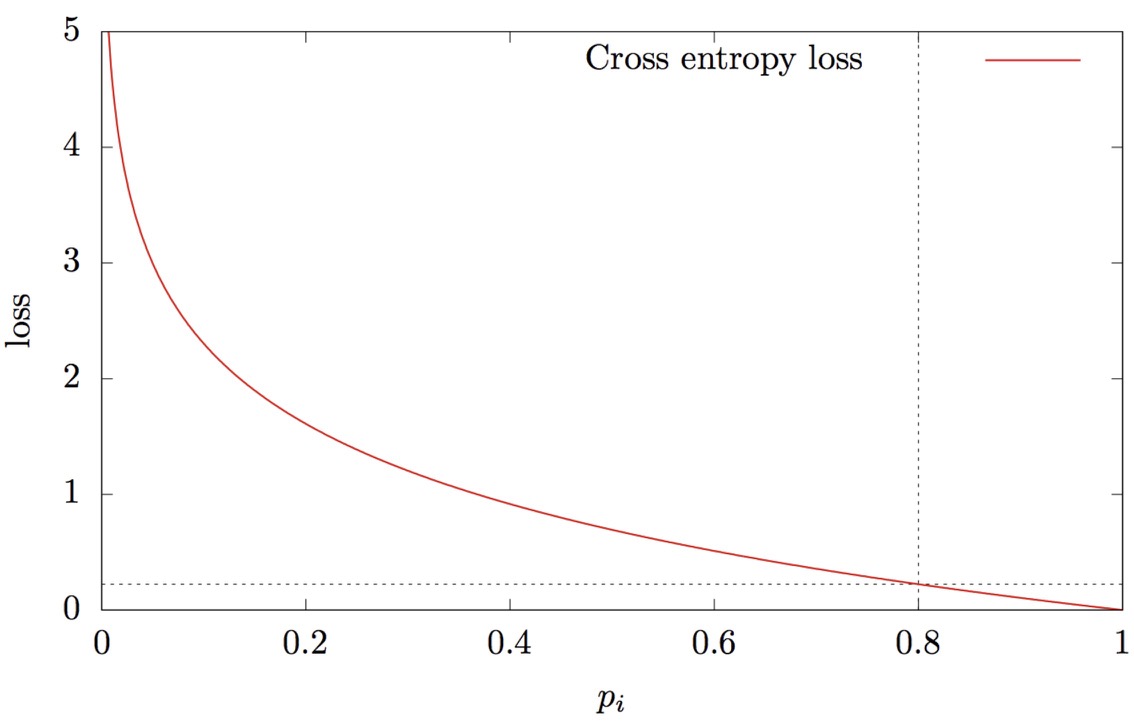
假如一个box 包含背景, 此box为背景的预测概率为0.8. 那么loss为: $-log(0.8) \approx 0.22$ . 若一张图片中只有10个真正的物体, 在 yolo-v3 的第三层输出, 共 8112 个box, 有10个box负责检测它们, 网络预测10个box为目标的概率很低,假如为0.05, 则每一个box 的损失 $-log(0.05) \approx 3$, 则10个box的总损失为30. 另外 8102 个box 都对应的是背景, 同时网络非常确信它们是背景 $p_t=0.9$, 每一个box 的损失为 0.1, 总损失为 8102 X 0.1 = 810.2.
因此, 从例子中可以看出, 网络很容易分类正确的背景提供的loss占据了主导地位, 同理, 梯度也占据了主导. 因此, 网络偏向于学习这些很容易分类正确的, 对于少数真正感兴趣的难样本却难以学习.
这正是 focal loss 要解决的问题. focal loss 放缩交叉熵损失,以便网络已经非常确定的所有简单示例对损失的贡献都较小,因此学习可以集中在少数感兴趣的难例上:
$$FL(p_t) = -(1-p_t) ^ {\gamma} log(p_t)$$
$(1-p_t) ^ {\gamma}$ 为调节因子, $\gamma$ 为可调聚焦参数. 下图为在多个$\gamma$ 下的loss 对比图:
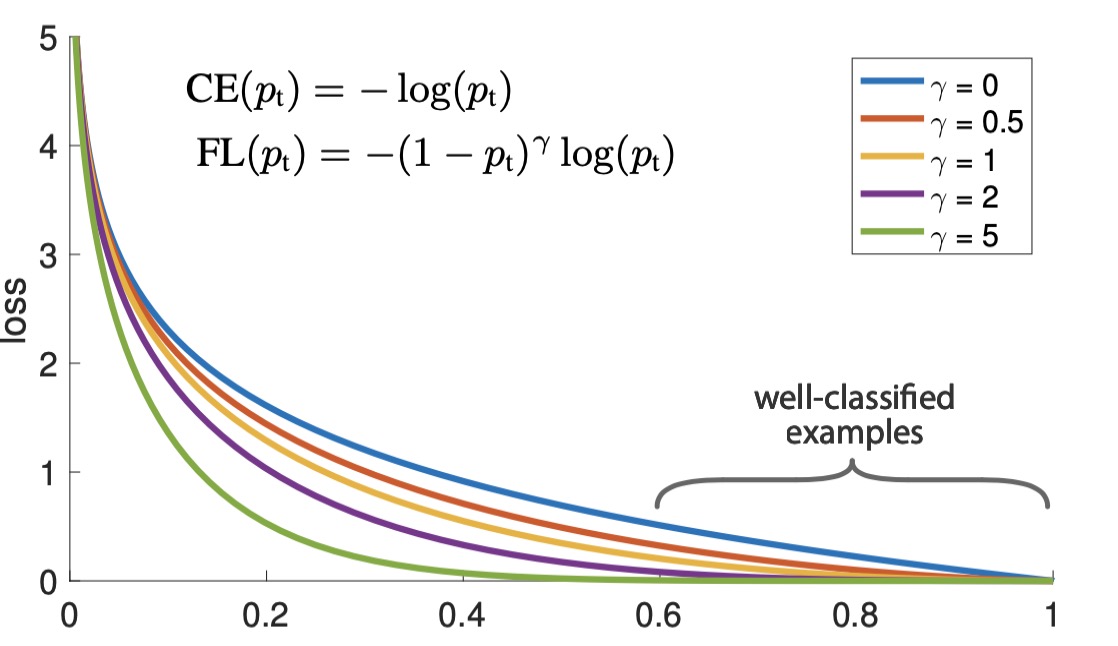
随着$\gamma$的增大, 较高预测概率提供的loss越来越小. 设$\gamma=2$, $p_t$ =0.9, 此时的loss为 0.001, 此时 8102个box的总损失为8.102, 缩小100倍. 而对于需要针对的目标, loss 并不会有太大影响.
对focal loss, 通过这种缩放, 大量易于分类的示例(主要是背景)不再占主导地位, 学习可以集中在少数感兴趣的困难样本上. 通过 focal loss, 理论上而言 one stage 目标检测的精度可以得到较大幅度的提升. focal loss 降低了易学习样本的损失比重,而yolo中背景占绝大数,属于易于学习的类别,focal loss 也起到了对平衡背景前景的作用。
在上诉focal loss的基础上, 作者采用的是加权 focal loss:
$$FL(p_t) = -\alpha _t (1-p_t) ^ {\gamma} log(p_t)$$

